सिध्द कीजिए कि किसी समबाहु त्रिभुज की माध्यिकाएँ समान होती हैं |
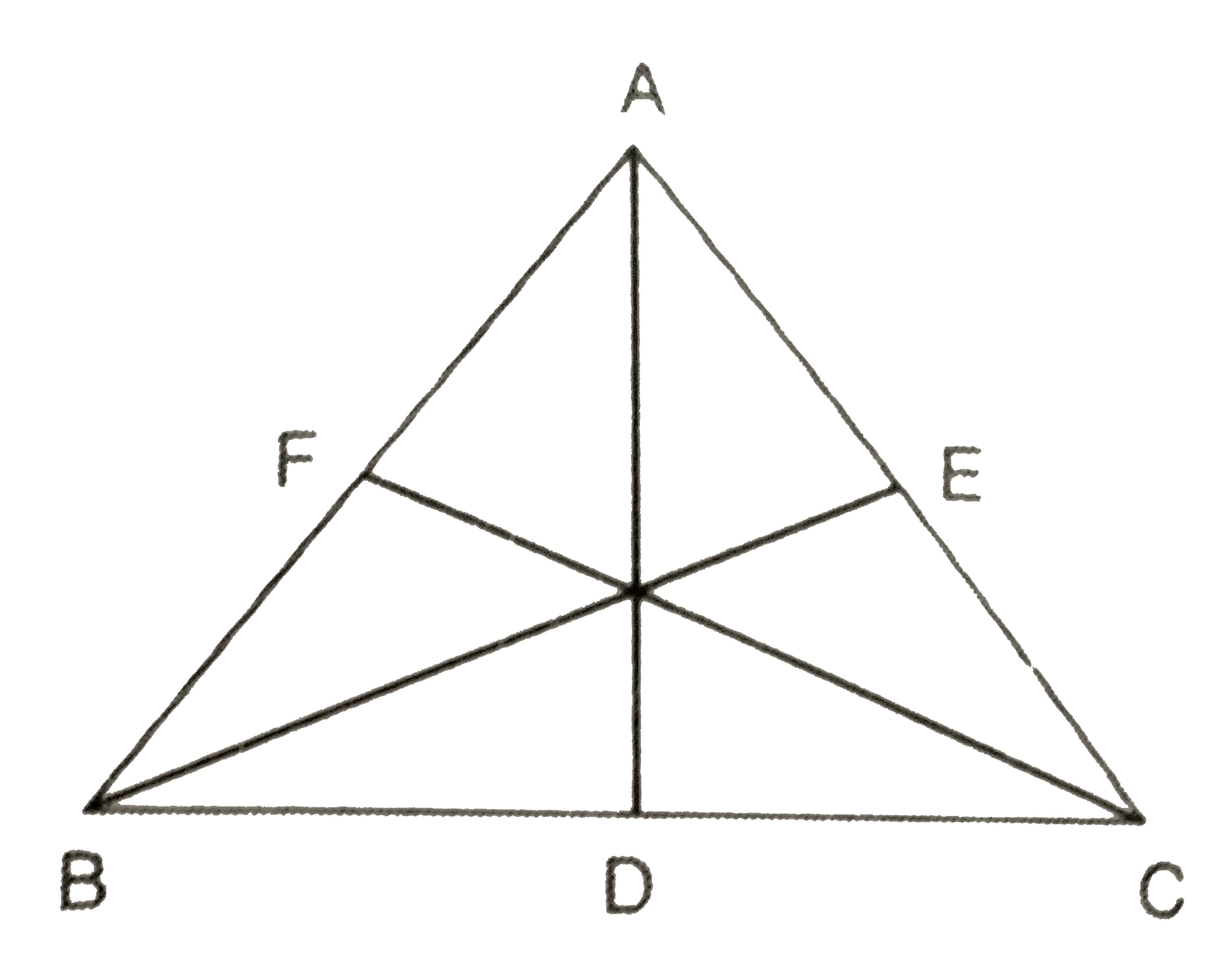
ΔABCएक समबाहु त्रिभुज है, जिसकी AD,BE तथा कफ माध्यिकाएँ हैं |
माना AB=AC=BC=x इकाई
त्रिभुज BFC तथा CEB में,हम देखते हैं कि
BF=CE [:'AB=AC⇒12AB=12AC⇒BF=CE]
∠ABC=∠ACB [प्रत्येक 60∘ के बराबर है]
तथा BC=BC [उभयनिष्ठ]
अतः भुजा-कोण-भुजा सर्वागसमता नियम से,
ΔBFC≅ΔCEB⇒BE=CF
इसी प्रकार, यह दर्शाया जा सकता है कि AB=BE
अतः AD=BE=CF
समान प्रश्न
किसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज की भुजाओ से समदूरस्थ बिंदु कहलाता है-
View Solutionदिखाइए कि किसी त्रिभुज में भुजाओं के लम्ब अर्धक संगामी होते हैं |
View Solutionसिद्ध कीजिए कि किसी समचतुष्फलक कि कोई दो सम्मुख कोरें परस्पर लम्ब होती हैं |
View Solutionकिसी त्रिभुज ABC की माध्यिकाएँ AD, BE, CF बिन्दु G पर मिलती हैं | दर्शाइए कि :
ΔAGB=ΔBGC=ΔCGA=13ΔABC.
View Solutionसिद्ध कीजिए कि सम्मिश्र संख्याओं 0, 2i और √3+i को निरूपित करने वाले बिंदु समबाहु त्रिभुज के शीर्ष है।
View Solutionकिसी त्रिभुज की माध्यिकाएँ …………. होती है ।
View Solutionयदि सम्मिश्र संख्याओं z, z + iz, iz से निरूपित बिन्दुओ से बनने वाले त्रिभुज का क्षेत्रफल 50 हो, तो सिध्द कीजिए कि |z|=10
View Solutionकिसी त्रिभुज की ऊँचाई और आधार क्रमशः 8 cm व 3 cm हैं, उसका क्षेत्रफल होगा :
View Solutionदो विशेष त्रिभुज : समबाहु तथा समद्विबाहु
View SolutionRevision |त्रिभुज एवं उसकी माध्यिकाएँ
View SolutionRevision |दो विशेष त्रिभुज : समबाहु तथा समद्विबाहु #!#एक त्रिभुज की दो भुजाओं की मापों का योग
View SolutionIf the height of an equilateral triangle is 10√3 cm, the area is:
यदि किसी समबाहु त्रिभुज की ऊंचाई 10√3 सेमी है, तो क्षेत्रफल ज्ञात करें |
View Solutionभूमिका |त्रिभुज का क्षेत्रफल |समबाहु त्रिभुज का क्षेत्रफल |समद्विबाहु त्रिभुज का क्षेत्रफल |सारांश
View Solutionत्रिभुज का क्षेत्रफल |समबाहु त्रिभुज का क्षेत्रफल |समद्विबाहु त्रिभुज का क्षेत्रफल |हीरोन का सूत्र |उदाहरण|सारांश
View Solution
