त्रिभुज ABC के अन्तः भाग में O कोई बिन्दु है | सिध्द करो कि
AB+BC+CA<2(OA+OB+OC)
Step by step video & image solution for त्रिभुज ABC के अन्तः भाग में O कोई बिन्दु है | सिध्द करो कि AB+BC+CA <2( OA+OB+OC) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023समान प्रश्न
If OABC be a regular tetrahedron such that OA2+BC2=OB2+CA2=OC2+AB2 then
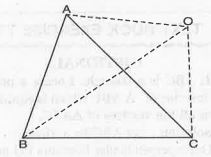
View SolutionIf O is point in the exterior of △ABC,show that 2(OA+OB+OC)>(AB+BC+CA)
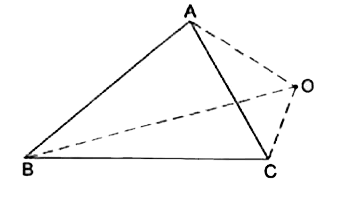
View SolutionO is any point in the exterior of a ΔABC. Prove that 2(OA+OB+OC)>(AB+BC+CA)
 .
.
View SolutionIf OABC is a tetrahedron such that OA2+BC2=OB2+CA2=OC2+AB2= then
View SolutionIf 0 is a point in the exterior of an ABC, then show that OA+OB +OC gt (1)/2 (AB + BC + CA)
View SolutionThe point O is outside the ∠ABC. Show that 2(OA+OB+OC)>AB+BC+CA.
View SolutionA point O lies inside a ΔABC. Show that OA+OB+OC>12(AB+BC+CA).
View SolutionThe OABC is a tetrahedron such that OA2+BC2=OB2+CA2=OC2+AB2,then
View Solution