In the figure,
(1) m (arc CE ) =54∘, m (arc BD ) 23∘, find measure of ∠CAE .
(2) If AB = 4.2 , BC = 5.4 , AE = 12.0, find AD .
(3) If AB = 3.6, AC = 9.0 , AD = 5.4 , find AE.

The correct Answer is:AD=3.36
Step by step video & image solution for In the figure, (1) m (arc CE ) = 54^(@), m (arc BD ) 23^(@), find measure of /_ CAE . (2) If AB = 4.2 , BC = 5.4 , AE = 12.0, find AD . (3) If AB = 3.6, AC = 9.0 , AD = 5.4 , find AE. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
The inequation represented by the graph given below is :
View SolutionIn the following figure, if O is the center of the circle and ¯¯¯¯¯¯AB is the diameter, then find ∠ACB.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E02_009_Q01.png" width="80%"gt
View SolutionIn the following figure, AD=5.6 cm, AE=(x+1)cm,AB=8.4cm and EC=(x−1)cm, find AC. Given that DE∣∣BC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E02_015_Q01.png" width="80%"gt
View SolutionIn the given figure, ¯¯¯¯¯¯AD and ¯¯¯¯¯¯BE intersect at C, such that BC = CE, ∠ABC=40∘ and ∠DEC=85∘. Find ∠BAC−∠CDE.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E04_027_Q01.png" width="80%"gt
View SolutionIn the given figure (not to scale), AC is the median as well as altitude to BD. In △ACE, AD is the median to CE. Which of the following is true?
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_010_Q01.png" width="80%"gt
View SolutionIn the figure (not to scale) AB = AC and BD = CD. Find ∠ADB
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E05_003_Q01.png" width="80%"gt
View SolutionIn the figure,
(1) m (arc CE ) =54∘, m (arc BD ) 23∘, find measure of ∠CAE .
(2) If AB = 4.2 , BC = 5.4 , AE = 12.0, find AD .
(3) If AB = 3.6, AC = 9.0 , AD = 5.4 , find AE.

View SolutionIn the adjoining figure,
(i) if m (arc CE) = 54∘ , m (arc BD) =23∘ , then find ∠CAE .
(ii) If AB = 4 . 2 , BC = 5 . 4 , AE = 12, then find AD
(iii) If AB 3 . 6 , AC = 9 . 0 , AD = 5 . 4 , then find AE.
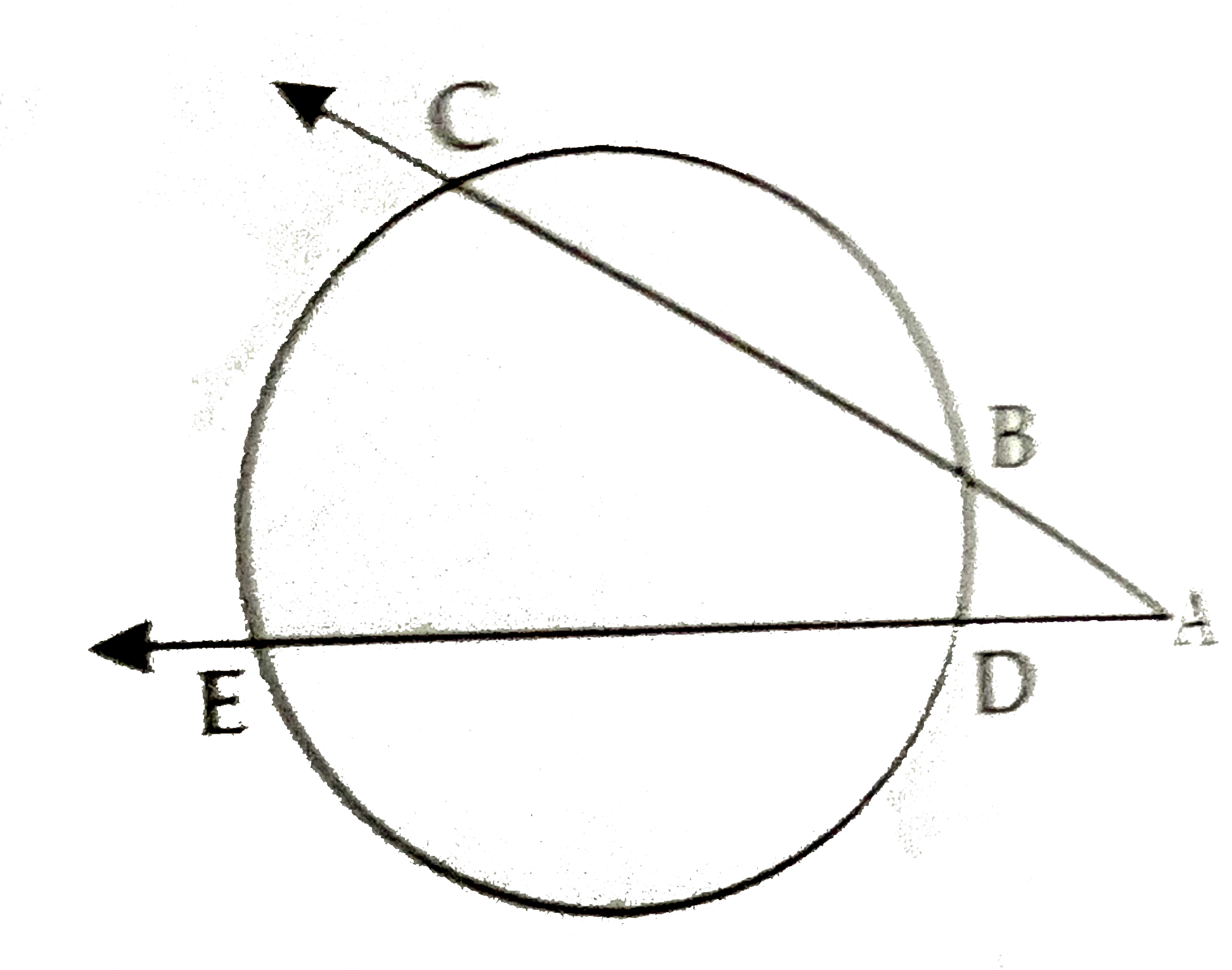
View Solution