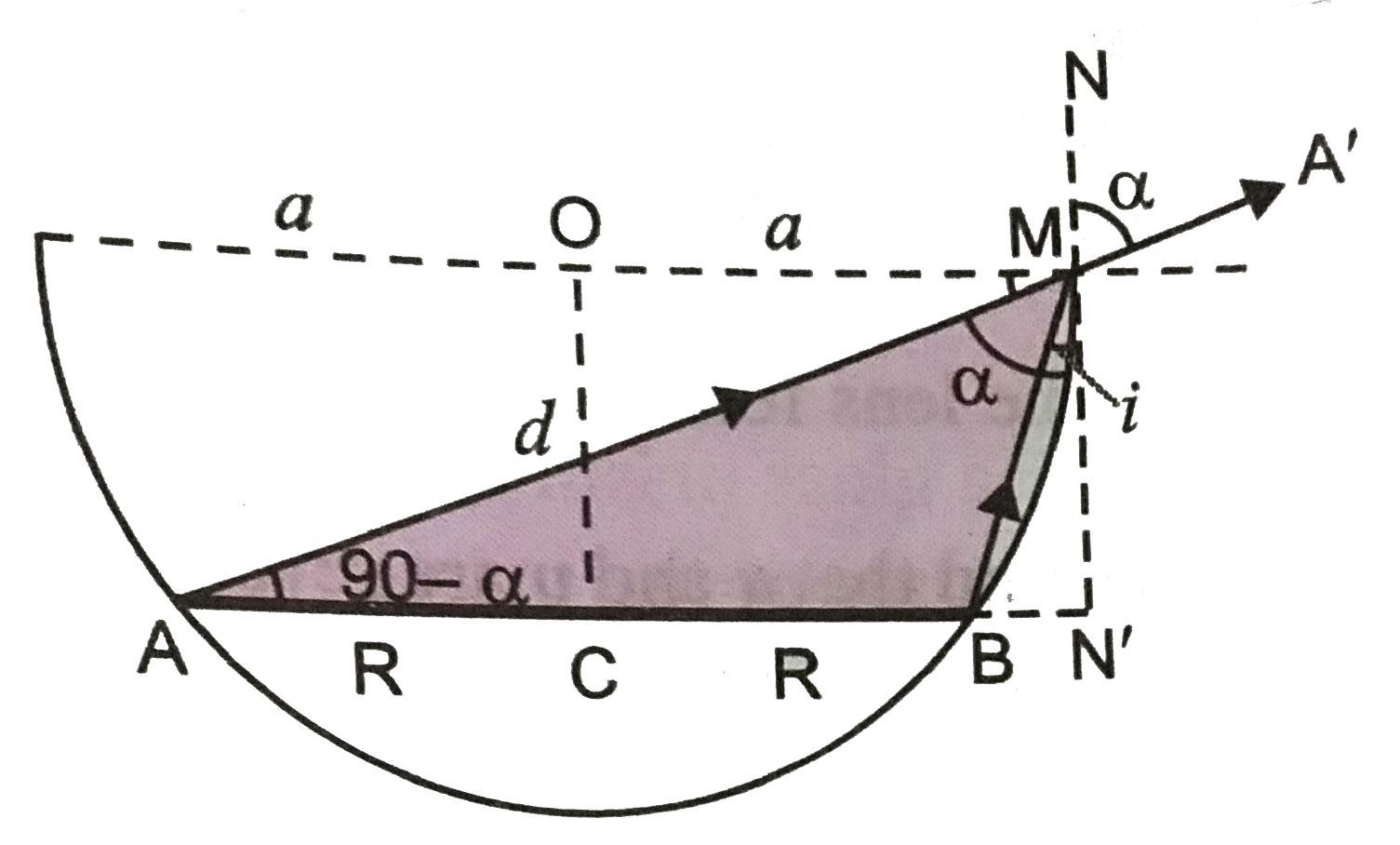
A circular disc of radius 'R' is placed co-axially and horizontally inside and opaque hemispherical bowl of radius 'a', Fig. The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index μ and the near edge of the dise becomes just visible. How far below the top of the bowl is the disc placed ?
 .
.
Video Solution
Text Solution
In Fig., we have shown an opaque hemisperical bowl of radius a with centre O.
A circular disc of radius R with centre C is placed co-axially and horizontally inside the bowl.We have to calculate OC=d.AMA' is the direction of incident index μ is filled in the bowl, the near edge B of the disc just becomes visible.
Here, BM is the incident ray, which is refracted along MA'
N' is normal to the horizontal surface of liquid in the bowl. i is the angle of incidence and r=∝ is the angle of refraction.
As refraction occurs at M in going from denser to rarer medium, therefore, according to Snell's law
1μ=sinisinr=sinisin∝ ....(i)
Now, sini=BN'BM=a−R√d2+(a−R)2 and sin∝=cos(90−∝)=AN'AM=a+R√d2+(a−R)2
Putting in (i), we get
1μ=a−R√d2+(a−R)2×√d2+(a+R)2a+R or μ×(a−R)√d2+(a+R)2=(a+R)√d2+(a−R)2
On simplifying, we get d=μ(a2−r2)√(1+R)2−μ(a−R)2.
|
Similar Questions
Knowledge Check
The coefficient of friction between an insect and a hemispherical bowl of radius r is μ. The maximum height to which the insect can crawl in the bowl is
Ar√1+μ2Br[1−1√1+μ2]Cr√1+μ2Dr[√1+μ2−1]A hemispherical bowl of radius r is placed in uniform electric field E . The electric flux passing through the bowl is
Aπr2EB2πrE2C4πr2ED4πrE2A hemispherical bowl of radius unity is filled up with water upto the depth 12. The valume of water in the bowl is
A27π24B5π24C3π4DNone of these
If R and r are the external and the internal radii of a hemispherical bowl, then what is the area of the ring, which forms the edge of the bowl (in sq. units)?
View SolutionA hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is5 cm. Find the outer curved surface area of the bowl.
View SolutionA hemispherical bowl of radius unity is filled up with water upto the depth 12. The valume of water in the bowl is
View SolutionThe radius of a hemispherical bowl is 6 cm. The capacity of the bowl is
(Take π=227)
View Solution
A small mass of 10 g lies in a hemispherical bowl of radius 0.5 m at a height of 0.1 m from the bottom of the bowl. The mass will be in equilibrius if the bowl rotates at an
View Solution
