ODBAC is a fixed rectangular conductor of negligible resistance (C0 is not connected) and 0P is a conductor which clockwise with an angular velocity ω (figure). The entire system is in a uniform magnetic field B whose direction is along the normal to the surface of the rectangular conductor ABDC. The conductor OP is in electirc contact with ABDC. The rotaating conductor has a resistance of λ per unit length. Find the current in the rotating conductor, as it rotates by 180∘.

The set up is shon in Fig Between time
t = 0 t=T8=π4ω, the rod OP will make contach
with side BD. At any time t: 0<t<π4ω, let the length
∴ Magnetic flux through the area ODQ is
ϕ=B×areaOQD=B×12QD×OD=B×12ltanθ×l
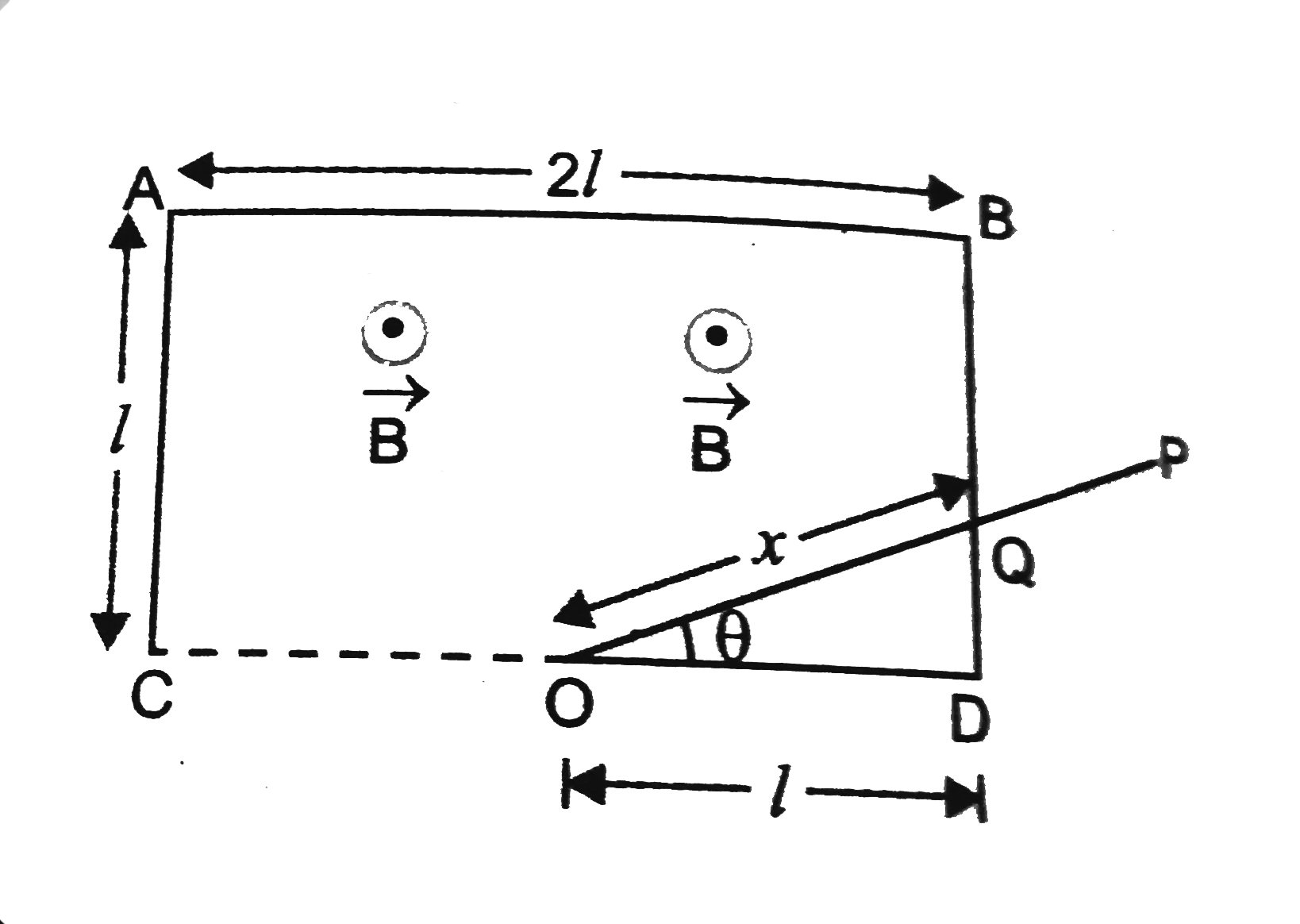
ϕ=12Bl2tanθ, where θ=ωt
Magnetic of emf generated, e=dϕdt=12Bl2ωsec2ωt
If R is resistance of the rod in contact, then induced current I=eR.
Now , R=λx=λlcosωt∴I=12Bl2ωsec2ωtλl/cosωt=Blω2λcosωt
For t=T8=π4ω to t=3T8=3π8, the rod is contact with
the side AB, as shown in Fig. Let the length of the rod in contant, OQ = x.
Magnetic flux linked with area ODBQ
ϕ=B×area of trapezium ODBQ =B(l2−l22tanθ), where θ=ωt

Magnitude of emf generated, e=dϕdt=12Bl2ωsec2ωt=12Bl2ωsec2ωttan2ωt
Induced current, I=eR=eλx=esinωtλl=12λ×Blωsinωt
For t=3T8=3π4ω to t=4T8=πω, the rod is in contact with
the side AC as shown in Fig.
Let the length of the rod in contact OQ = x.
Magnetic flux linked with area ODBAQ
ϕ=B× [area of rectangular ABDC - area of ΔOQC]
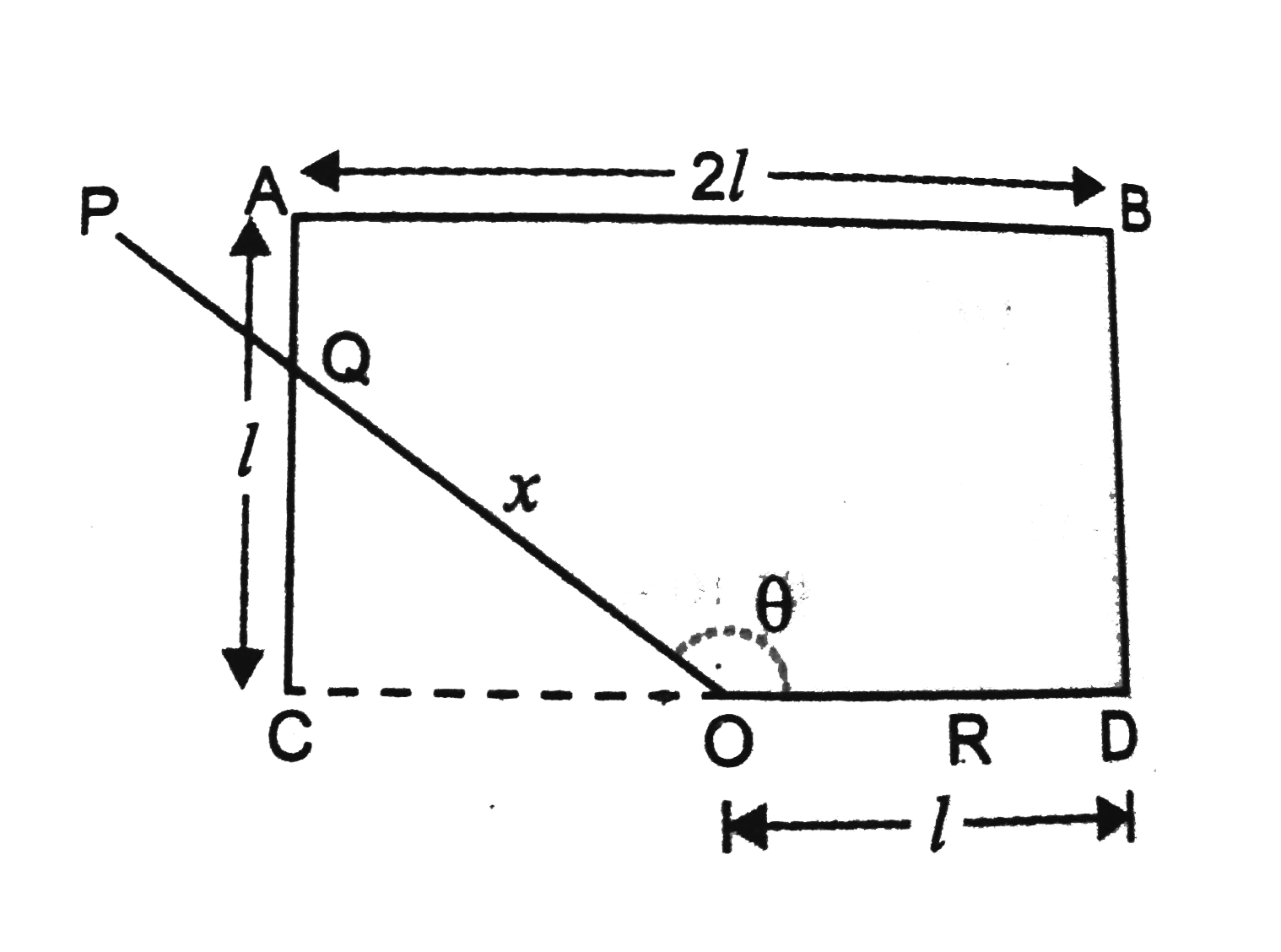
ϕ=B[2l2−l22tanωt]
Magnitude of induced emf, e=dϕdt=ddtB(2l2−l22tanωt)=Bωl2sec2ωt2tan2ωt
Induced current, I=eR=eλx=esinωtλl=Blω2λsinωt
Similar Questions
ODBAC is a fixed rectangular conductor of negligible resistance (C0 is not connected) and 0P is a conductor which clockwise with an angular velocity ω (figure). The entire system is in a uniform magnetic field B whose direction is along the normal to the surface of the rectangular conductor ABDC. The conductor OP is in electirc contact with ABDC. The rotaating conductor has a resistance of λ per unit length. Find the current in the rotating conductor, as it rotates by 180∘.

View SolutionThe resistance of a conductor is
View Solution
Knowledge Check
For an ideal conductor thermal resistance is .
AunityBinfinityCzeroD1000Resistance of conductor depends on
Aapplied potential difference across the conductor and electric current passing through the conductorBlength and area of cross- section of the conductorCtemperature of the conductorDboth 2 and 3The resistance of a conductor depends on its
AMaterial of conductorBLength of conductorCArea of cross-section of conductorDAll of these
A conductor of length T'is rotated about one of its ends at a constant angular speed 'ω' in a plane perpendicular to a uniform magnetic field B. Plot graphs to show variations of the emf induced across the ends of the conductor with (i) angular speed o and (ii) length of the conductor i.
View SolutionResistance of a conductor does not depends on
View SolutionThe electrical resistance of a conductor
View SolutionThe resistance of a conductor depends on its
View SolutionThe resistance of a conductor increases with
View Solution
