A ray of light the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism. Given angle of prism is A.
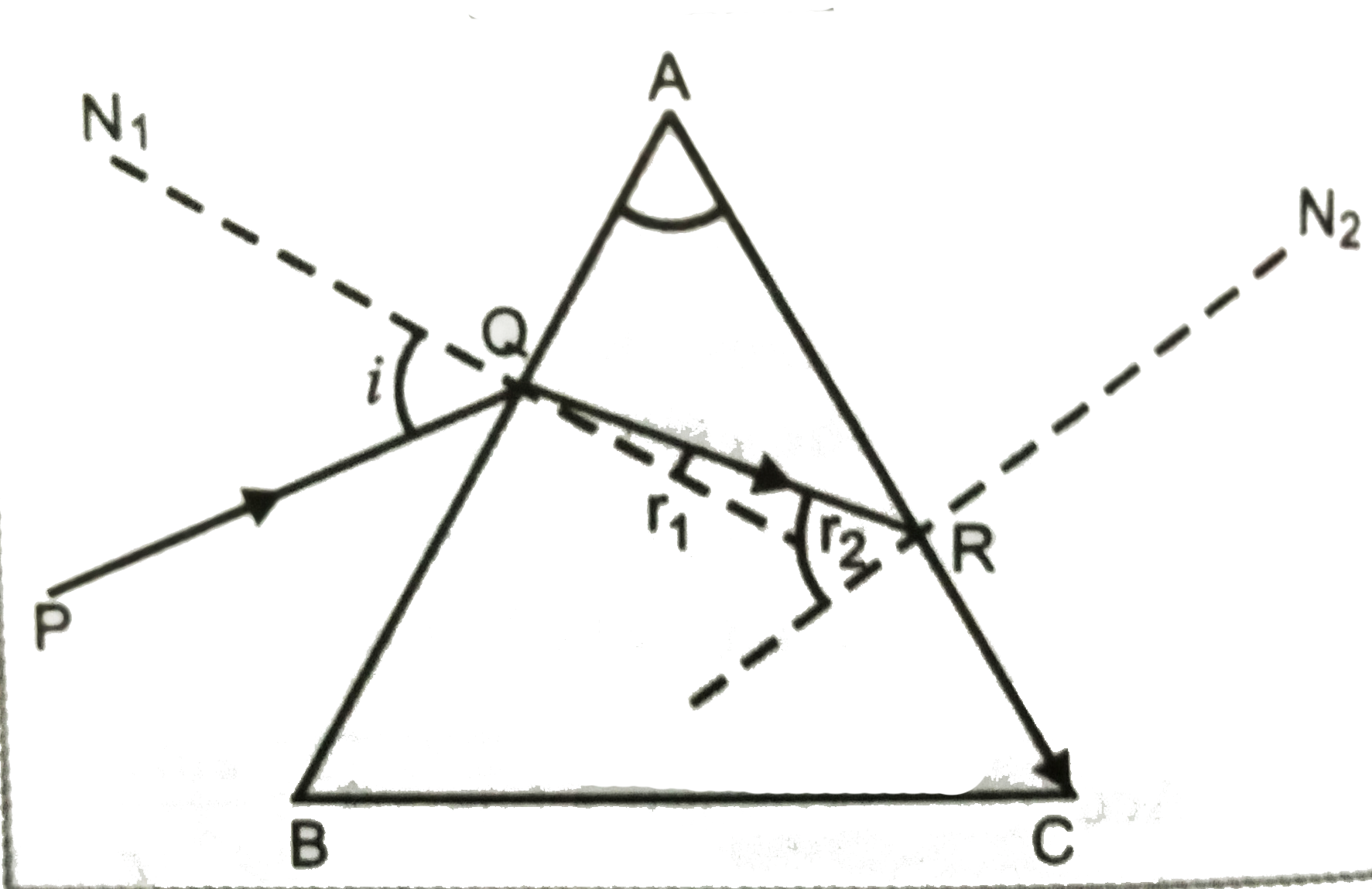
As no ray emerges from face AC of prism, therefore, refracted ray QR must be undergoing total internal reflection at R.
∴r2=C.
As sinC=1μ=sinr2
∴Musinr2=1. …(i)
sinI=μsinr1 ...(ii)
but r1+r2=A∴r1=A−r2
∴ form (ii), sini=μsin(A−r2)=μ(sinAcosr2−cosAsinr2)
sini=μsinAcosr2−μsinr2cosA
using (i), sini=μsinAcosr2−cosA
From (i), sinr2=1μ cosr2=√1−sin2r2=√1−1μ2
From (iii), sini=μsinA√1−1μ2−cosA.
Hence, i=sin−1[μsinA√1−1μ2−cosA]
Similar Questions
A ray of light enters the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism, given angle of prism is A.
View SolutionA ray of light incident normally on the first face of a glass prism of refractive index 1.6 just emerges from the other face. Find the angle of the prism.
View Solution
Knowledge Check
A glass prism has a refractive angle of 90∘ and a refractive index of 1.5. A ray is incident at an angle of 30∘. The ray emerges from an adjacent face at an angle of
A60∘B30∘C45∘Dthe ray does not emergeLight falls at normal incidence on one face of a glass prism of refractive index √2. Then the angle of emergence when the angle of the prism is 45∘
A45°B60°C15°D90°Light ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
Asin−1(√3−12)Bsin−1(√2−12)Csin−1(√32)Dsin−1(23√3)
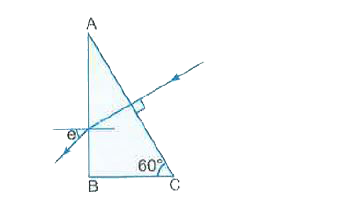
Calculate the angle of emergence (e) of the ray of light incident normally on the face AC of a glass prism ABC of refractive index √3. How will the angle of emergence change qualitatively, if the ray of light emerges from the prism into a liquid of refractive index 1.3 instead of air ?
View SolutionA ray of light falls on a glass prism at a angle of incidence of 30∘. Find the direction of the emergent ray if the angle of the prism is 60∘ and refractive index is 1.50
View SolutionA ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View SolutionFor a ray of light refracted through a prism of angle 60∘, the angle of incidence is equal to the angle of emergence, each equal to 45∘. Find the refractive index of the material of the prism.
View SolutionLight ray is incident on a prism of angle A=60∘and refractive indexμ=√2.the angle of incidence at which the emergent ray grazes the surface is given by
View Solution
