सिद्ध कीजिए कि त्रिभुज की माध्यिकाएँ संगामी होती हैं । यह भी सिद्ध कीजिए कि संगमन बिंदु माध्यिकाओं को 2 : 1 के अनुपात में विभाजित करता हैं ।
वीडियो समाधान
लिखित उत्तर
माना त्रिभुज के शीर्ष A, B व C हैं जहां
A ≡(x1,y1,z1),B≡(x2,y2,z2)वC=(x3,y3,z3)
माना BC का मध्य - बिंदु D हैं
तब D के निर्देशांक = (x2+x32,y2+y32,z2+z32)
अब माना बिंदु G रेखाखण्ड AD को 2:1 के अनुपात में अन्तः विभाजित करता हैं ।
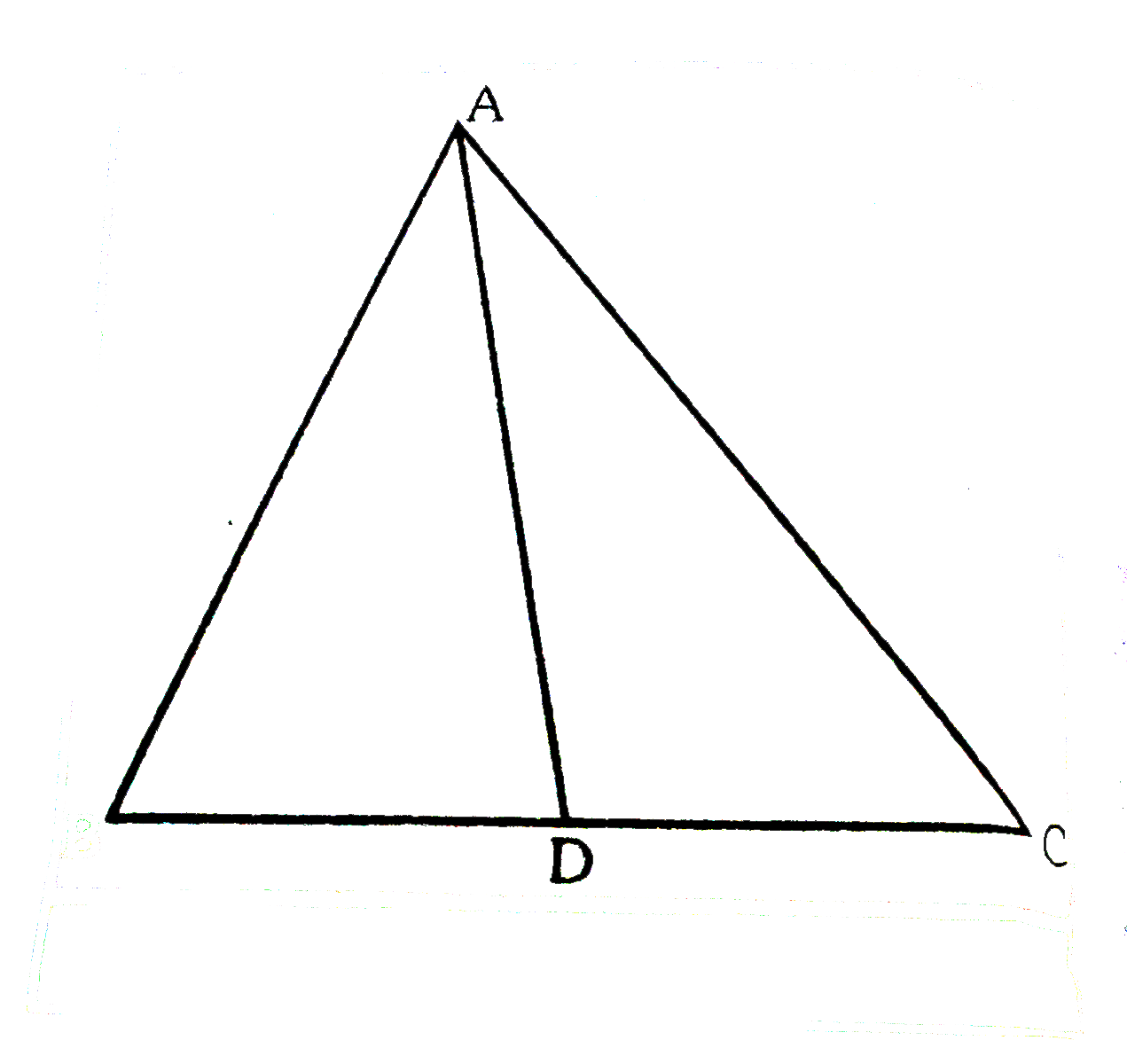
तब , G के निर्देशांक
=⎛⎜
⎜⎝2(x2+x32)+1⋅x13,2(y2+y32)+1⋅y13,2(z2+z32)+1⋅z13⎞⎟
⎟⎠
= (x1+x2+x33,y1+y2+y33,z1+z2+z33)
स्पष्टतः G, त्रिभुज ABC की अन्य दो माध्यिकाओं पर भी स्थित हैं ।
⇒ त्रिभुद की माध्यिकाएँ संगामी होती हैं तथा G प्रत्येक माध्यिका को 2 : 1 के अनुपात में विभाजित करता हैं ।
|
समान प्रश्न
सिद्ध कीजिए कि सम्मिश्र संख्याओं 0, 2i और √3+i को निरूपित करने वाले बिंदु समबाहु त्रिभुज के शीर्ष है।
View Solutionयदि बिन्दु (a,b),(a',b') और (a−a',b−b') संरेख हो तो सिद्ध कीजिए कि
ab'=a'b.
साथ ही यह भी सिद्ध कीजिए कि इन बिन्दुओं से होकर जाने वाली रेखा मुलबिन्दु से होकर जाती है।
View Solutionसिद्ध कीजिए कि f(x)=ax,o<a<1,R में ह्रासमान है।
View Solutionसिद्ध कीजिए कि [→a×→b→a×→c→d]=[→a.→d][→a→b→c]
View Solutionसिद्ध कीजिए कि [→a×→b→a×→c→d]=(→a.→d)[→a→b→c]
View Solutionसिद्ध कीजिए कि [ˆiˆjˆk]+[ˆiˆkˆj]=0
View Solutionसिद्ध कीजिए कि (→a×→b)×(→c×→d)=[→a→b→d]→c−[→a→b→c]→d
View Solutionयदि A, B, C, D समष्टि (space) में चार बिन्दु हैं, तो सिद्ध कीजिए कि |AB×CD+BC×AD+CA×BD|=4 ( त्रिभुज ABC का क्षेत्रफल )
View Solution
