निम्न में प्रत्येक के लिए सत्यमान सारणी बनाइये
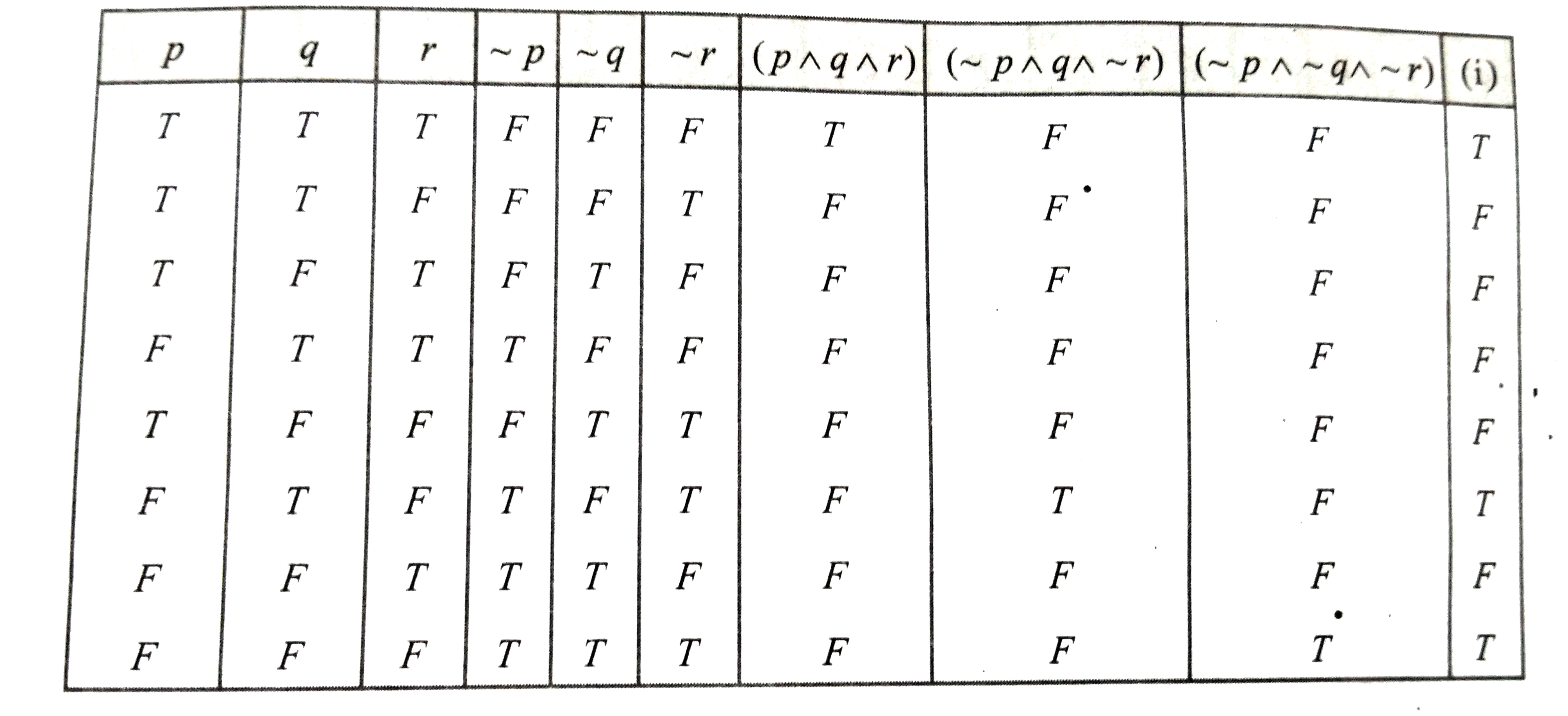
(p∧q∧r)∨(~p∧q∧~r)∨(~p∧~q∧~r)
Text Solution
सत्यमान सारणी निम्न प्रकार होगी
|
Similar Questions
agreed p^^(q^^r)=(p^^q)vv(p^^r) This is the rule
View SolutionObserve the following statements
I : The dual of [~p∧q)]∨[p∧{~(q∨~s)}] is [~(p∨q)]∧[p∨{~(q∧~s)}]
II : The dual of ~p∧[(~q)∧(p∨q)∧~r] is ~p∨[~q)∨(p∧q)∨~r]
The true statements in the above is/are :
View Solutionमाना p,q,r तीन सरल कथन है, तो ~(p∨q)∨~(p∨r)=??
View SolutionThe logical statement [~(~p∨q)∨(p∧r)]∧(~q∧r) is equivalent to (a) (~p∧~q)∧r (b) ~p∨r (c) (p∧r)∧~q (d) (p∧~q)∨r
View SolutionNegation of (~p∧~q)∨(~p∨r) is
View SolutionThe dual of the statement
~(p∨q)∧[p∨(q∧~r)] is
View SolutionIf S(p,q,r)=(~p)∨[−(q∧r)] is a compound statement, then S(~p,~q,~r) is a)~S(p,q,r) b)S(p,q,r) c)p∨(q∧r) d)p∨(q∨r)
View SolutionLet p, q, r be three simple statements. Then, ~(p∨q)∨~(p∨r) is equal to a)(~p)∧(~q∨~r) b)(~p)∧(q∧r)c)p∧(q∨r)d)p∨(q∧r)
View Solution

