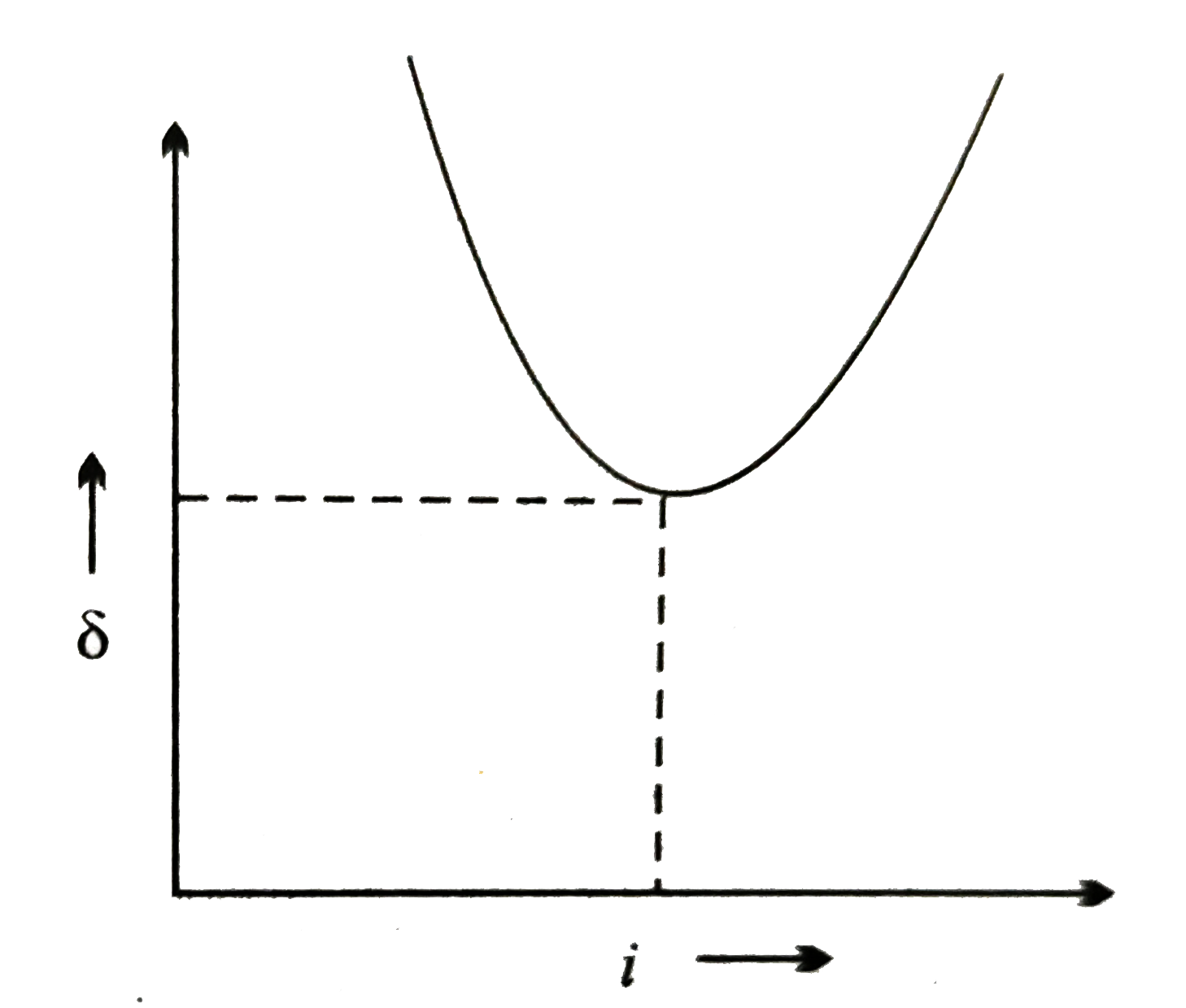
अपवर्तनांक कोण A के काँच प्रिम से गुजरने वाली एकवर्णी प्रकाश के अपवर्तन को प्रदर्शित करने लिए किरण आरेख खींचिए । अतः काँच के अपवर्तनांक i−δ के लिए प्रिम कोण व न्यूनतम विचलन कोण के पदों में व्यंजक कीजिए इसके लिए ग्राफ भी खींचिए।
माना की एक प्रिज्म ABC का मुख्या परिच्छेद, AB व AC अपवर्तनक पृष्ठ तथा A प्रिज्म का कोण है । यदि कोई प्रकाश किरण प्रिज्म पर PQ दिशा में अपवर्तित होती है तो वह QR दिशा में पवर्तित होकर RS दिशा में निर्गत होगी। बिंदु Q तथा R से अभिलम्ब MO व NO है तथा आपतित किरण PQ को आगे की ओर तथा निर्गत किरण RS को पीछे की ओर बढ़ाने पर एक दूसरे को बिंदु T पर काटते है।
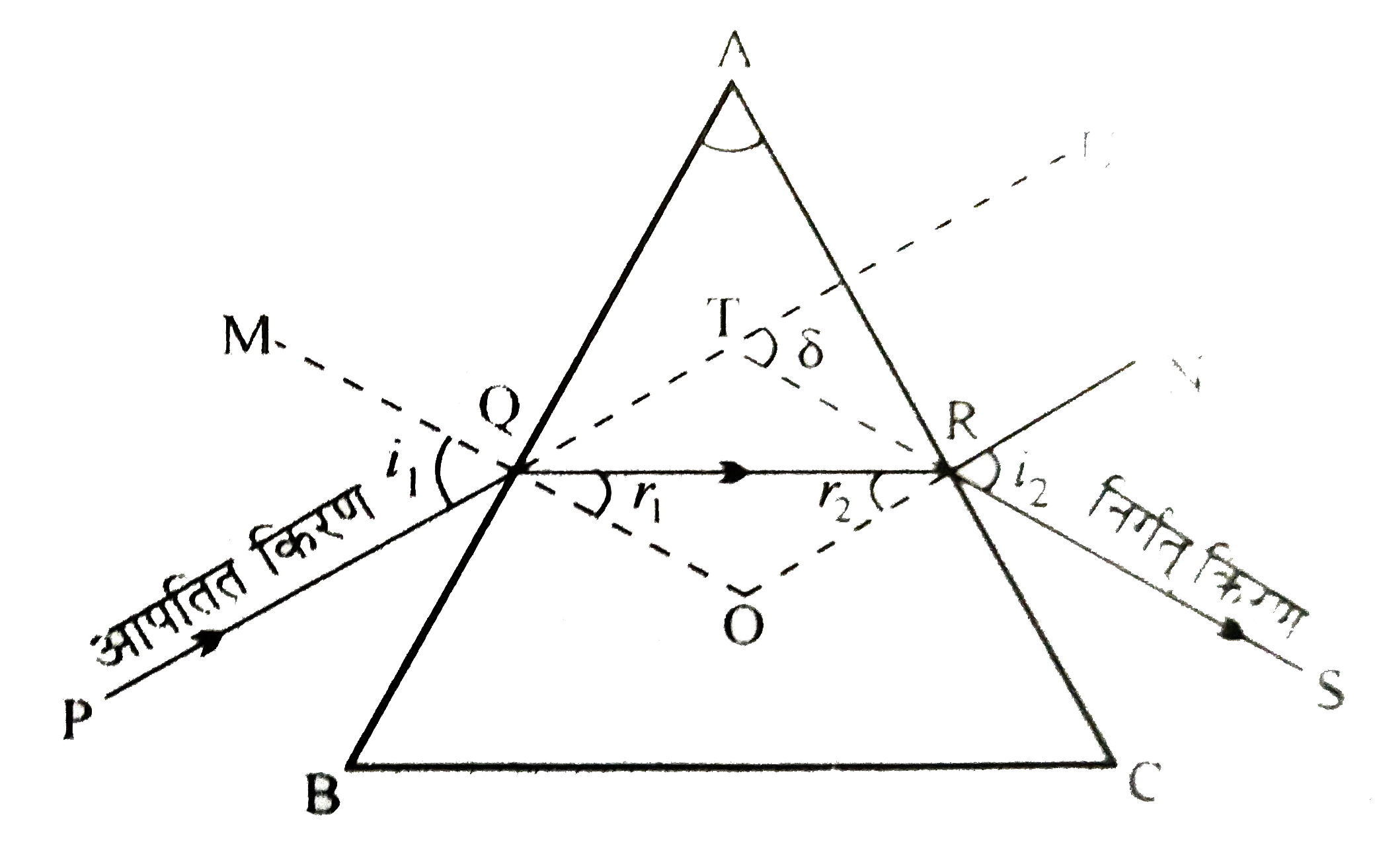
∴ विचलन कोण
δ=∠UTS=∠TQR+∠TRQ
=(il−r1)+(i2−r2) ...(i)
जहाँ ∠MPQ=ii,∠RQO=r1
∠QRO=r2 तथा ∠NRS−i2 है ।
न्यूनतम विचलन की स्थिति में,
δ=δm,il=i2=i तथा r1=r2=r (मानलो) समीकरण (1) में मान रखने पर,
∴δm=(i−r)+(r−i)
या δm=2i−2r...(2)
चतुर्भुज AQOR में
∠AQO+∠ARO=180∘ ...(3)
अतः शेष कोण ∠A+∠QOR=180∘ ...(4)
अब ΔOQR से
∠QOR+r1+r2=180∘ ...(5)
समीकरण (4) और (5) से,
∠A+∠QOR=∠QOR+r1+r2
या ∠A=r1+r2
न्यूनतम विचलन की स्थिति में,
A=r1+r=2r
∴r=A2
समीकरण (2) में मान रखने पर,
δ(m)=2i−A
या 2i=A+δm
याi=A+δm2
अब स्नेल के नियम से,
,u=sinisinr
i और r के मान रखने पर,
μ=sinA+δm2sinA2
Similar Questions
रेखाएँ एवं कोण#!# पूर्ण अध्याय के लिए महत्वपूर्ण प्रश्न
View Solutionत्रिभुजों की समरूपता |त्रिभुजों की समरूपता के लिए कसौटियाँ |AA (कोण कोण) कसौटी |त्रिभुजों की समरूपता के लिए कसौटियाँ |NCERT प्रश्नावली |सारांश
View Solutionत्रिभुजों की समरूपता |त्रिभुजों की समरूपता के लिए कसौटियाँ - भाग 1 |AA (कोण - कोण) कसौटी |त्रिभुजों की समरूपता के लिए कसौटियाँ - भाग 2 |NCERT प्रश्नावली |सारांश
View Solutionत्रिभुजों की समरूपता |त्रिभुजों की समरूपता के लिए कसौटियाँ - भाग 1 |AA (कोण - कोण) कसौटी |त्रिभुजों की समरूपता के लिए कसौटियाँ - भाग 2 |NCERT प्रश्नावली |सारांश
View Solutionत्रिभुजों की समरूपता |त्रिभुजों की समरूपता के लिए कसौटियाँ - भाग 1 |AA (कोण - कोण) कसौटी |त्रिभुजों की समरूपता के लिए कसौटियाँ - भाग 2 |NCERT प्रश्नावली |सारांश
View Solutionएकसमान व असमान त्वरण के लिए ग्राफ
View Solutionकिसी भी कोण के लिए त्रिकोणमितीय फलन |प्रश्न |OMR
View Solutionत्रिपरमाण्विक अणु YXY के लिए कौनसे बंध कोण θ के परिणामस्वरूप द्विध्रुव आघूर्ण अधिकतम होगा?
View Solution

