A disc of radius 10cm rotates in XY plane about an axis passing through its centre and perpendicular to the plane. At a particlular moment a point A on the disc has an acceleration →aA=−6ˆIm/s2.
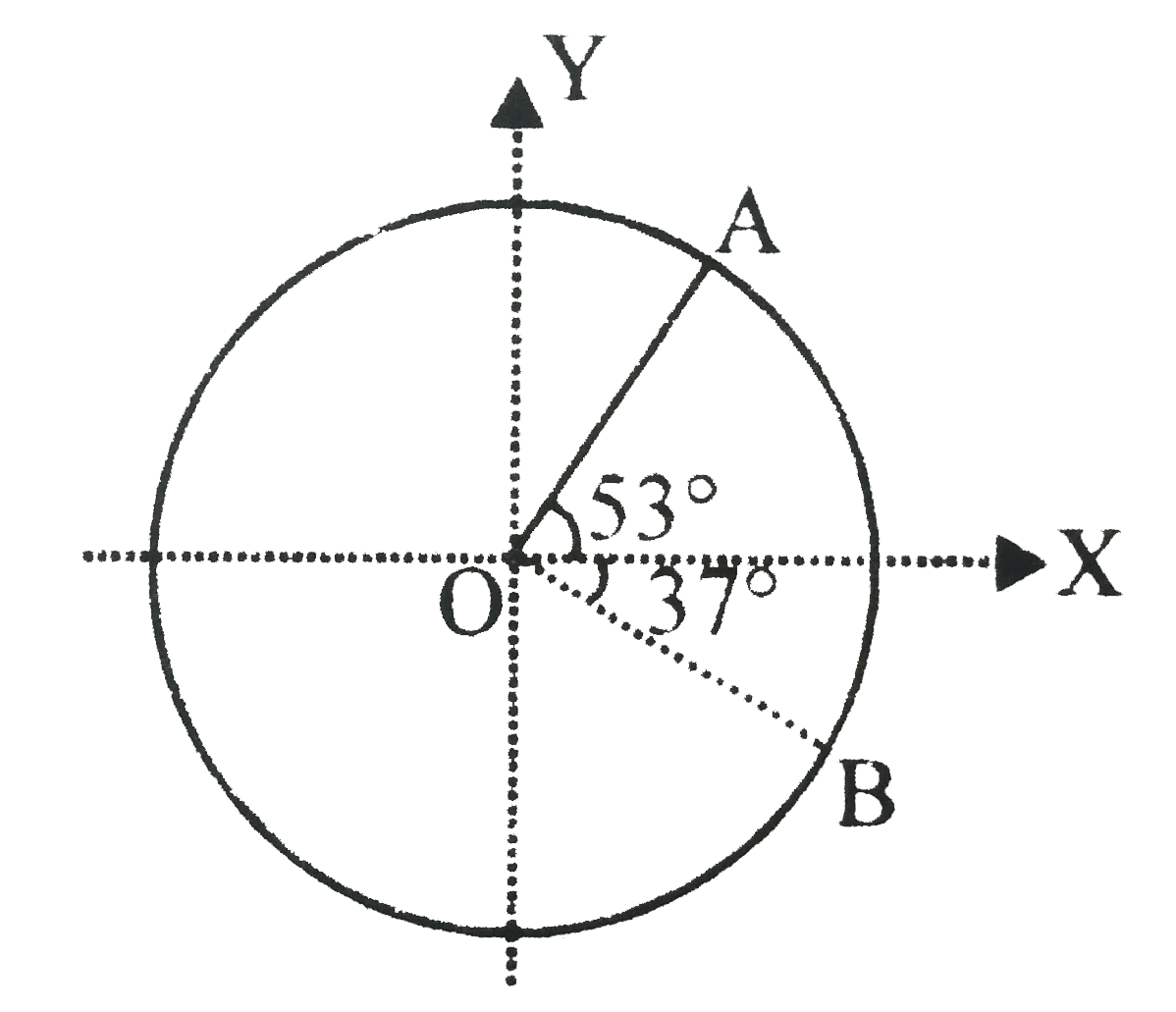
The linear acceleration of point B on disc is :
6ˆim/s2
−6ˆim/s2
6ˆjm/s2
−6ˆjm/s2
The correct Answer is:B
Step by step video, text & image solution for A disc of radius 10 cm rotates in XY plane about an axis passing through its centre and perpendicular to the plane. At a particlular moment a point A on the disc has an acceleration vec a_(A) = - 6 hat I m//s^(2). The linear acceleration of point B on disc is : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
The radius of gyration of a uniform disc of radius R, about an axis passing through a point (R )/(2) away from the centre of disc, and perpendicular to the plane of disc is:
View SolutionFind the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionCalculate the moment of inertia of uniform circular disc of mass 500 g, radius 10 cm about : the axis through the centre of the disc and perpendicular to its plane
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point R2 away from the centre of disc, and perpendicular to the plane of disc is:
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point (R )/(2) away from the centre of disc, and perpendicular to the plane of disc is:
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point (R )/(2) away from the centre of disc, and perpendicular to the plane of disc is:
View Solution

