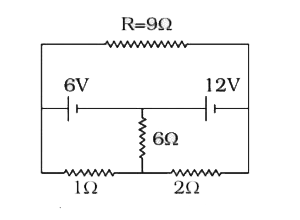
Shown a circuit with known resistance R,R1 and R2 neglect the resistance of the conducting wires and internal resistance of current source The magnitude of electrotive force E1 each that the currect l through the resistance R in zero will be

A
E(R2R1)
B
E(R1R2)
C
E(R1+R2R2)
D
E(R1R1+R2)
Video Solution
Text Solution
The correct Answer is:c
The distribution of current in the various arms as per Kirchhoff's first law, has been
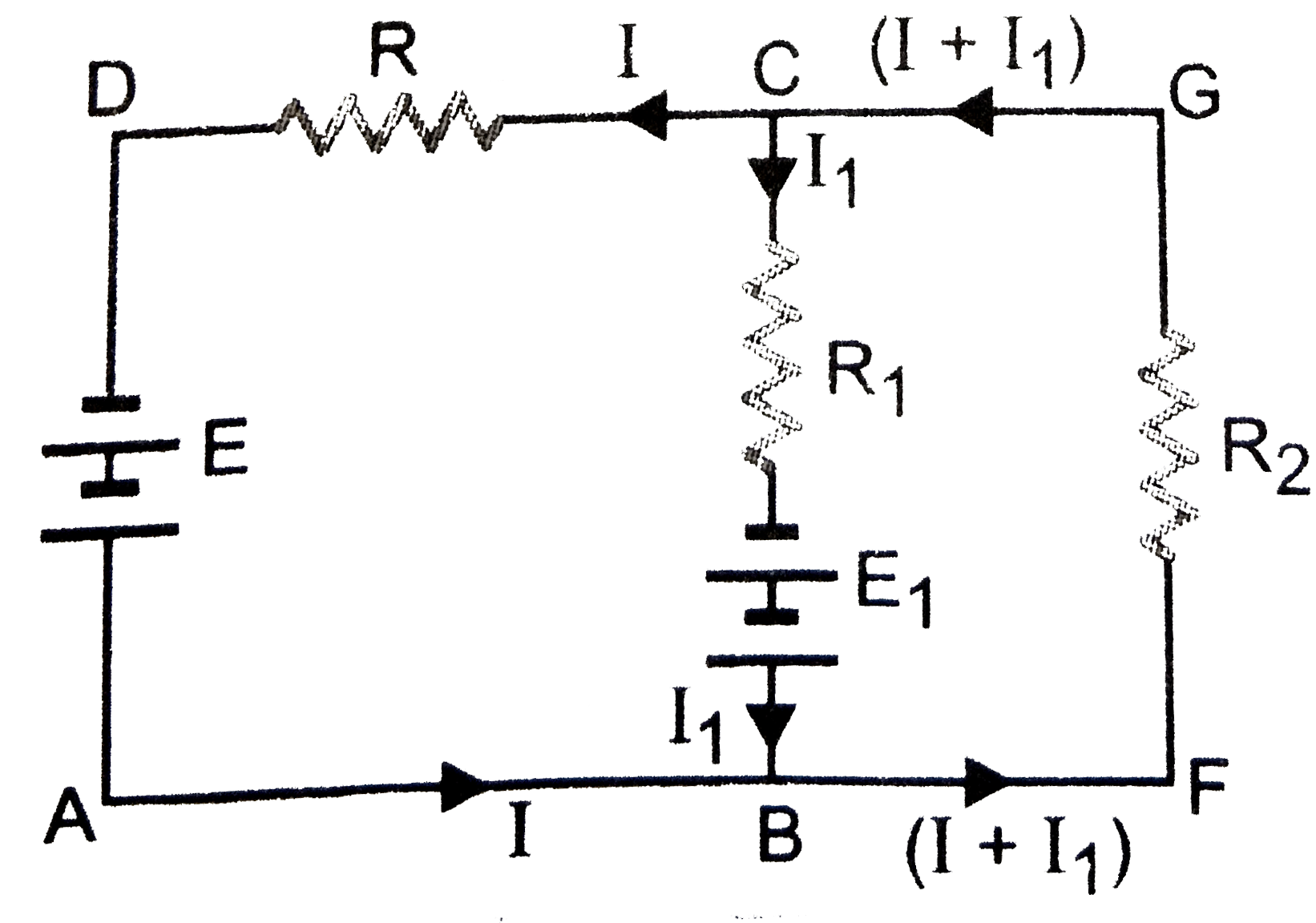
Using Kirchhoff's second law in closed circuit ABFGCDAZ and BFGCB we have
E=(I+I1)R2+IR
and E1=(I+I1)R2+I1R1
Putting I=0 , we have :
E=I1R2andE1=I1(R1+R2)
∴E1=ER2(R1+R2)
|
Similar Questions
Knowledge Check
The current in the resistance R will be zero if
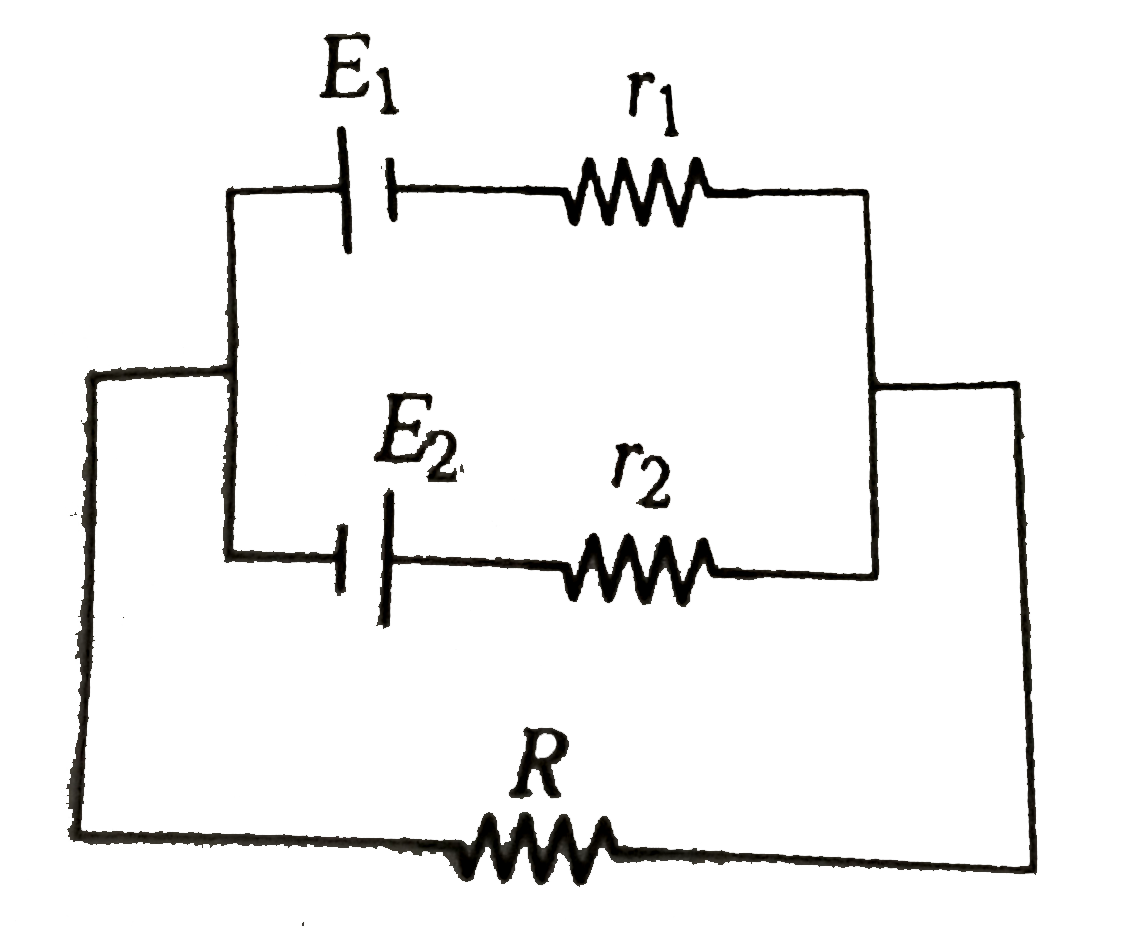 AE1r1=E2r2BE1r1=E2r2C(E1+E2)r1=E1r1D(E1−E2)r1=E2r1
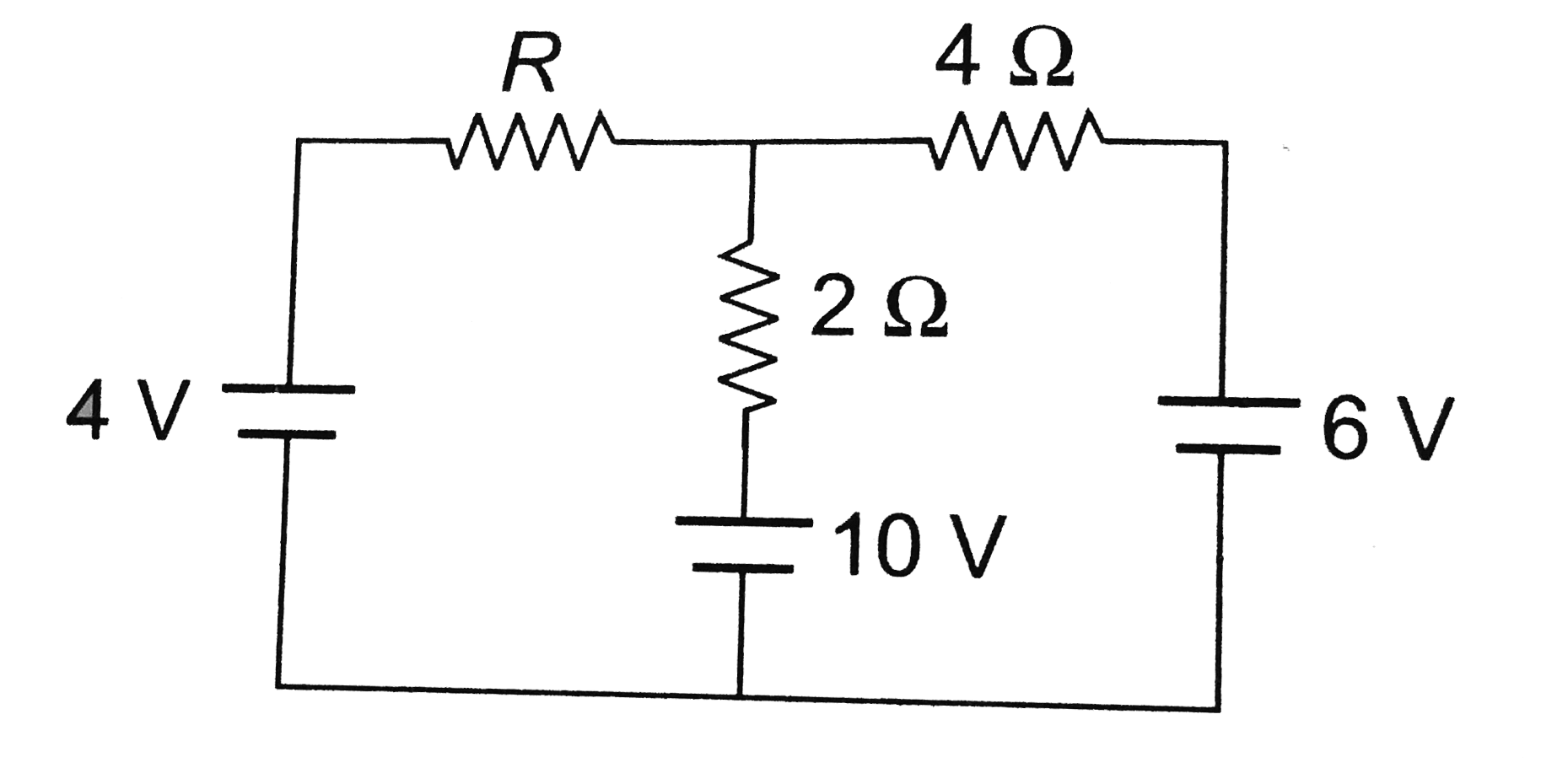
AE1r1=E2r2BE1r1=E2r2C(E1+E2)r1=E1r1D(E1−E2)r1=E2r1In the circuit shown in the given figure, the resistances R1andR2 are respectively
 A14Ωand40ΩB40Ωand44ΩC40Ωand30ΩD14Ωand30Ω
A14Ωand40ΩB40Ωand44ΩC40Ωand30ΩD14Ωand30ΩEach resistance of the circuit shown in figure is r. The equivalent resistance between A and B is
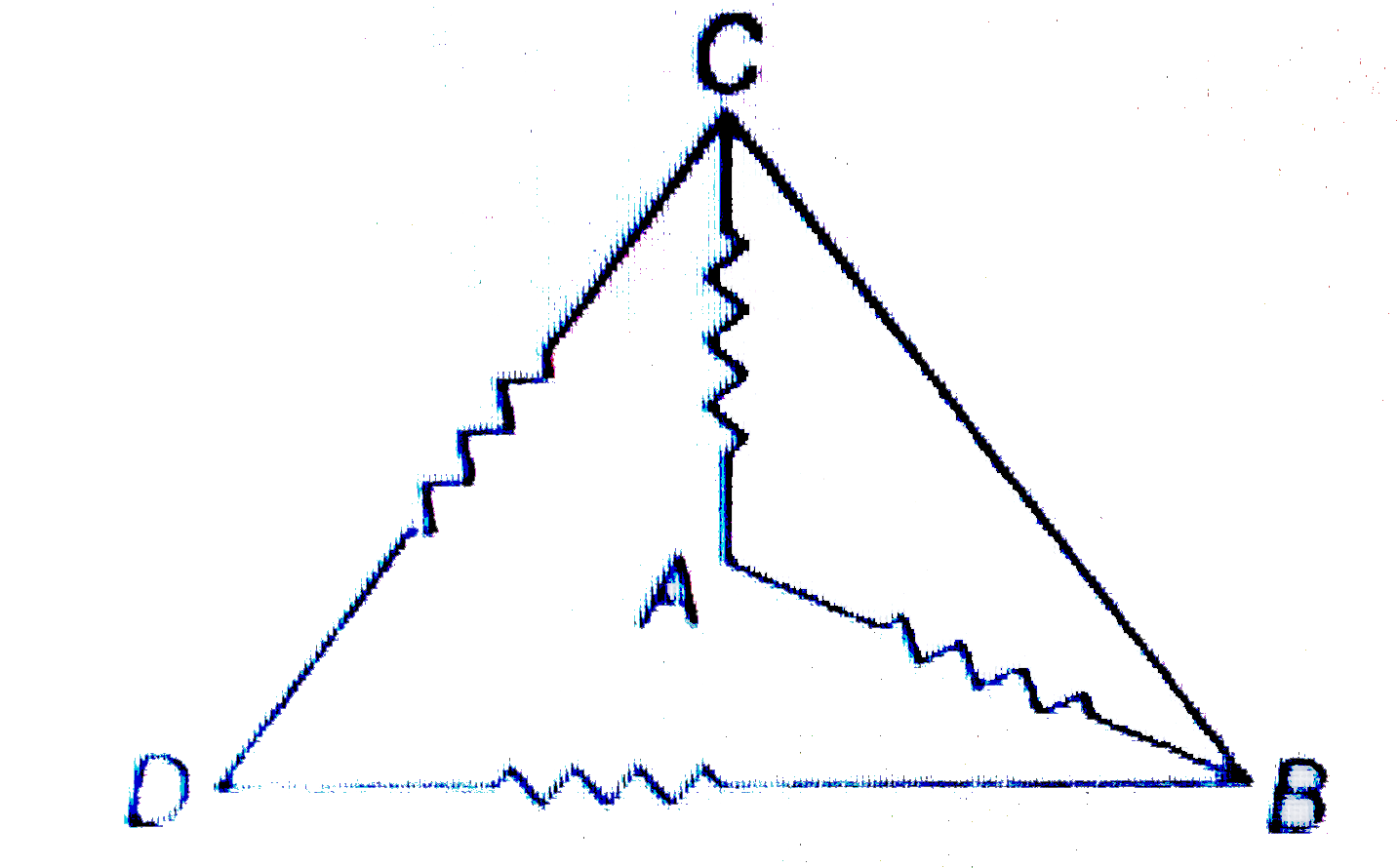 ArBr/4Cr/2D5r/8
ArBr/4Cr/2D5r/8
If resistors of resistance R1 and R2 are connected in parallel,then resultant resistance is "
View SolutionFor what value of R in circuit , current through 4Ω resistance is zero.
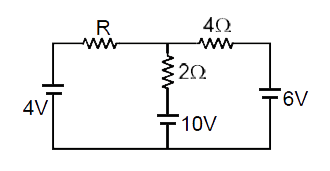
View SolutionIn the circuit shown in figure resistance of each wire is r. Net resistance across

View SolutionAn external resistance R is connected to a cell of internal resistance r. The current in the circuit is maximum when
View SolutionA battery is of emt E and internal resistance r. The value of external resistance R so that the power across eternal resistance is maximum :
View Solution