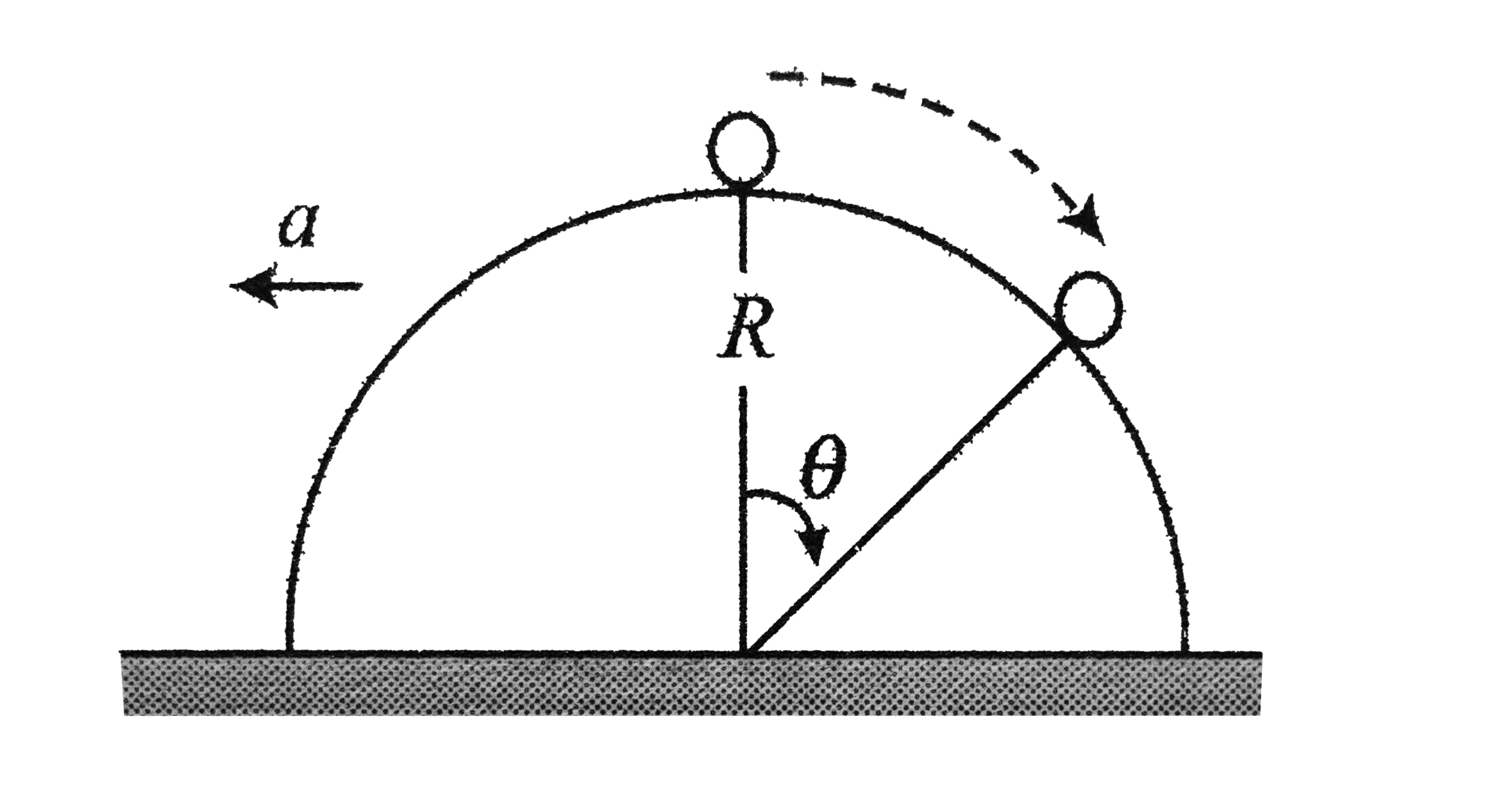
A small body is placed on the top of a smooth sphere of radius R. Then the sphere is imparted a constant acceleration w0 in the horizontal direction and the body begins sliding down. Find:
(a) the velocity of the body relative to the sphere at the moment of break-off,
(b) the angle θ0 between the vertical and the radius vector drawn from the centre of the sphere to the break-off point, calculate θ0 for w0=g.
In the problem, we require the velocity of the body, relative to the sphere, which itself moves with an acceleration w0 in horizontal direction (say towards left). Hence it is advisible to solve the problem in the frame of sphere (non-inertial frame).
At an arbitary moment, when the body is at an angle θ with the vertical, we sketch the force diagram for the body and write the second law of motion in projection form
Fn=mwn
or, mgcosθ−Nmw0sinθ=mv2R (1)
At the break off point, N=0, θ=θ0 and let v=v0 so the Eq. (1) becomes,
v20R=gcosθ0−w0sinθ0 (2)
From, Ft=mwt
mgsinθ−mw0cosθ=mvdvds=mvdvRdθ
or, vdv=R(gsinθ+w0cosθ)dθ
Integrating, v0∫0vdv=θ0R0(gsinθ+w0cosθ)dθ
v202R=g(1−cosθ0)+w0sinθ0 (3)
Note that the Eq. (3) can also be obtained by the work-energy theorem A=ΔT (in the frame of sphere)
therefore, mgR(1−cosθ0)+mw0Rsinθ0=12mv20
[here mw0Rsinθ0 is the work done by the pseudoforce (−m→w0)]
or, v202R=g(1−cosθ0)+w0sinθ0
Solving Eqs. (2) and (3) we get,
v0=√2gR/3 and θ=cos−1[2+k√5+9k23(1+k2)], where k=w0g
Hence θ0∣w0=g=17∘

Similar Questions
A small body A starts sliding off the top of a smooth sphere of radius R. Find the angle θ (figure) corresponding to the point at which the body breaks off the sphere, as well as the break-off velocity of the body.

View SolutionA small body of mass m=0.30kg starts sliding down from the top of a smooth sphere of radius R=1.00m. The sphere rotates with a constant angular velocity ω=6.0rad/s about a vertical axis passing through its centre. Find the centrifugal force of inertia and the Coriolis force at the moment when the body breaks off the surface of the sphere in the reference frame fixed to the sphere.
View Solution
Knowledge Check
A small body of mass 'm' is placed at the top of a smooth sphere of radius 'R' placed on a horizontal surface as shown, Now the sphere is given a constant horizontal acceleration a0=g. The velocity of the body relative to the sphere at the moment when it loses contact with the sphere is
 A√gR3B√2gR3C√5gR3D√7gR3
A√gR3B√2gR3C√5gR3D√7gR3A small ball is placed at the top of a smooth hemispherical wedge of radius R. If the wedge is accelerated with an acceleration a, find the velocity of the ball relative to wedge as a function of θ.
 A√2R[g(1−sinθ)+aRcosθ]B√2R[g(1+cosθ)−aRsinθ]C√2R[g(1−cosθ)+aRsinθ]D√2R[g(1+sinθ)−aRcosθ]
A√2R[g(1−sinθ)+aRcosθ]B√2R[g(1+cosθ)−aRsinθ]C√2R[g(1−cosθ)+aRsinθ]D√2R[g(1+sinθ)−aRcosθ]A body rest on the top of a hemisphere of radius R. What will be the least horizontal velocity imparted to it , if it has to leave the hemisphere without sliding down?
A√2gRB√5gRC√gRD√3gR
Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
View SolutionA particle rests on the top of a smooth hemisphere of radius r. It is imparted a horizontal velocity of √ηgr. Find the angle made by the radius vector joining the particle with the vertical at the instant the particle losses contact with the sphere.

View SolutionA smooth spehre of radius R is made to translate oin a straight line with a constant acceleration a. A particle kept on the top of the sphere is released rom there at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a functon of the angle θ it slides.
View SolutionA block of mass m is placed on a smooth sphere of radius R. It slides when pushed slightly. At what vertical distance h, from the top, will it leave the sphere?
View SolutionA smooth spehre of radius R is made to translate oin a straight line with a constant acceleration a. A particle kept on the top of the sphere is released rom there at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a functon of the angle θ it slides.
View Solution
