A small body A starts sliding from the height h down an inclined groove passing into a half-circle of radius h/2 (figure).

Assuming the friction to be negligible, find the velocity of the body at the highest point of its trajectory (after breaking off the groove).
To complete a smooth vertical track of radius R, the minimum height at which a particle starts, must be equal to 52R (one can proved it from energy conservation). Thus in our problem body could not reach the upper most point of the vertical track of radius R/2. Let the particle A leave the track at some point O with speed v (figure). Now from energy conservation for the body A in the field of gravity:
mg[h−h2(1+sinθ)]=12mv2
or, v2=gh(1−sinθ) (1)
From Newton's second law for the particle at the point O., Fn=mwn,
N+mgsinθ=mv2(h/2)
But, at the point O the normal reaction N=0
So, v2=gh2sinθ (2)
From (3) and (4), sinθ=23 and v=√gh3
After leaving the track at O, the particle A comes in air and further goes up and at maximum height of it's trajectory in air, it's velocity (say →v) becomes horizontal (figure). Hence, the sought velocity of A at this point.
v′=vcos(90−θ)=vsinθ=23√gh3

Similar Questions
A small bead of mass M slides on a smooth wire that is bent in a circle of radius R. It is released at the top of the circular part of the wire (point A in the figure) with a negligibly small velocity. Find the height H where the bead will reverse direction
View SolutionA body slides down an inclined surface which ends into a vertical loop of radius R = 40cm.
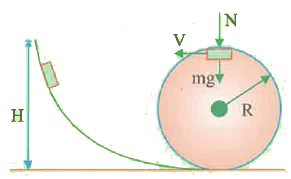
What must be the height H of the inclined surface for the body so that it does not leave contact with the surface even at the uppermost point of the loop? Assume friction to be absent.
View SolutionA body slides down an inclined plane after being released from rest from a height h and finally it describes a circle of radius r instead of travelling along a horizontal floor. For what minimum value of h , can the particle describe that motion ? Ignore friction.
View SolutionA body slides from rest by its own weight on the surface for a frictionless incline through a vertical height 'h'. Calculate its velocity.
View SolutionStarting from rest , a body slides down at 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
View SolutionStarting from rest, a body slides down a 45^(@) inclined plane in twice the time it itakes to slide the same distance in the absence of friction. They the coefficient of friction between the body and the inclined plane is
View SolutionA small body A starts sliding from the height h down an inclined groove passing into a half-circle of radius h/2 (figure).

Assuming the friction to be negligible, find the velocity of the body at the highest point of its trajectory (after breaking off the groove).
View SolutionA small bead of mass M slides on a smooth wire that is bent in a circle of radius R. It is released at the top of the circular part of the wire (point A in the figure) with a negligibly small velocity. Find the height H where the bead will reverse direction
View Solution

