A thin uniform square plate with side l and mass M can rotate freely about a stationary vertical axis coinciding with one of its sides. A small ball of mass m flying with velocity v at right angles to the plate strikes elastically the centre of it. Find:
(a) the velocity of the ball v′ after the impact,
(b) the horizontal component of the resultant force which the axis will exert on the plate after the impact.
(a) In the process of motion of the given system the kinetic energy and the angular momentum relative to rotation axis do not vary. Hence it follows that
12mv2=12mv′2+12(Ml23)ω2
and mvl2=mv′l2+Ml23ω
From these equations we obtain
v′=(3m−4M3m+4M)v. and ω=4vl(1+4m/3M)
As →'v↑⏐⏐↑⏐⏐→v, so in vector form →'v=(3m−4M3m+4M)→v
(b) Obviously the sought force provides the centripetal acceleration to the C.M. of the rod and is
Fn=mwcn
=Mω2l2=8Mv2l(1+4M/3m)2
Similar Questions
A thin uniform square plate with side l and mass M can rotate freely abouta stationary vertical axis coinciding with one of its sides . A small ball of mass m flying with velocity v at right angles to the plate strikes elastically to the centre of it. Find the velocity of the ball v'after the impact and the horizontal component of the force which the axis will exert on the plate after the impact.
[3m−4M3m+4Mv,72Mm2v2l(3m+4m)2]
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View Solution
Knowledge Check
A ball of mass m1 is moving with velocity 3v. It collides head on elastically with a stationary ball of mass m2 . The velocity of both the balls become v after collision. Then the value of the ratio m2m1 is
A1B2C3D4A ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
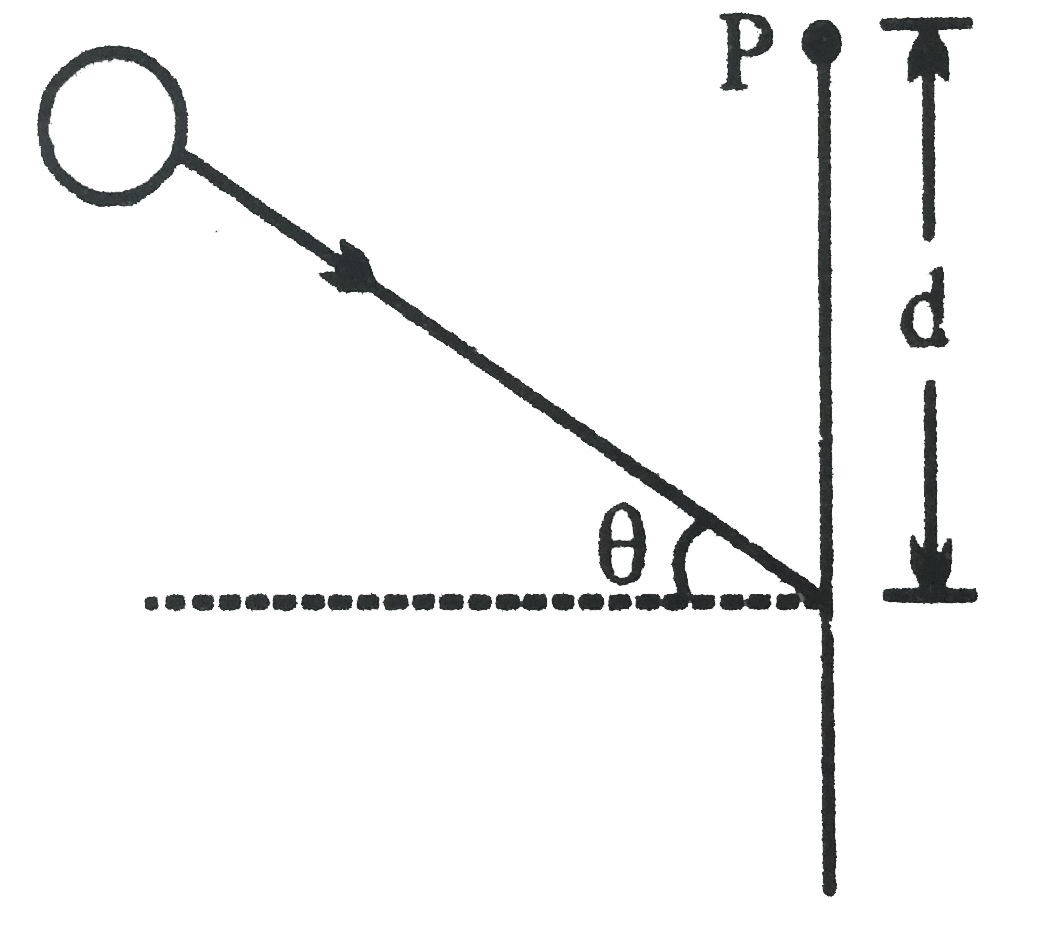 .A2mvdB2mvdcosθC2mvdsinθDzero
.A2mvdB2mvdcosθC2mvdsinθDzeroA ball of mass 2m impinges directly on a ball of mass m, which is at rest. If the velocity with which the larger ball impringes be equal to the velocity of the smaller mass after impact then the coefficient of restitution :-
A13B34C12D25
A ball moving with a velocity v strikes a wall moving toward the wall with a velocity u. An elastic impact occurs. Determine the velocity of the ball after the impact. What is the cause of the change in the kinetic energy of the ball ? Consider the mass of the wall to be infinitely great.
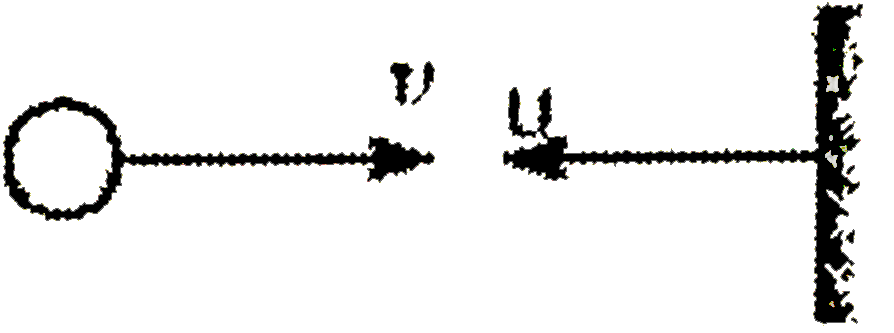
View SolutionA rod of mass 12 m and length l lying on a smooth horizontal plane can rotate freely about a stationary, vertical axis passing through the rod's end. A particle of mass m moving along the plane with speed v0 hits the rod's end perpendicularly and gets stuck there. Find the angular velocity of the system.

View SolutionA ball of mass 2m impinges directly on a ball of mass m, which is at rest. If the velocity with which the larger ball impinges be equal to the velocity of the smaller mass after impact then the coefficient of restitution :-
View SolutionA square plate of side / has mass M. What is its moment of inertia about one of its diagonals ?
View SolutionA thin uniform plate shaped as an equilateral triangle with a height 'h' performs small oscillations about the horizontal axis coinciding with one of its sides. The time period of oscillation is…..
View Solution
