A horizontally oriented uniform rod AB of mass m=1.40kg and length l0=100cm rotates freely about a stationary vertical axis OO′ passing through its end A. The point A is located at the middle of the axis OO′ whose length is equal to l=55cm. At what angular velocity of the rod the horizontal component of the force acting on the lower end of the axis OO′ is equal to zero? What is in this case the horizontal component of the force acting on the upper end of the axis?
The total centrifugal force can be calculated by,
l0∫0ml0ω2xdx=12ml0ω2
Then for equilibrium,
(T2−T1)l2=mgl02
and, T2+T1=12ml0ω2
Thus T1 vanishes, when
ω2=2gl, ω=√2gl=6rad/s
Then T2=mgl0l=25N

Similar Questions
A rod of mass M and length L lying horizontally is free to rotate about a vertical axis through its end. A horizontal force F on the rod at the other end, the force always remains perpendicular to the rod. Find the angular velocity of the rod when it has turned an angle π/2.
View SolutionA thin horizontal uniform rod AB of mass m and length l can rotate freely about a vertical axis passing through its end A. At a certain moment, the end B starts experiencing constant force F which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. Find the angular velocity of the rod as a function of its rotation angle ϕ counted relative to the initial position.
View Solution
Knowledge Check
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]A horizontally orientied unifrom copper rod of length l is rotating about a vertical axis passing through its centre. Calculate the rotated frequency at which the rod ruptures. Breaking or rupture strength of copper is σ and density of copper is ρ.
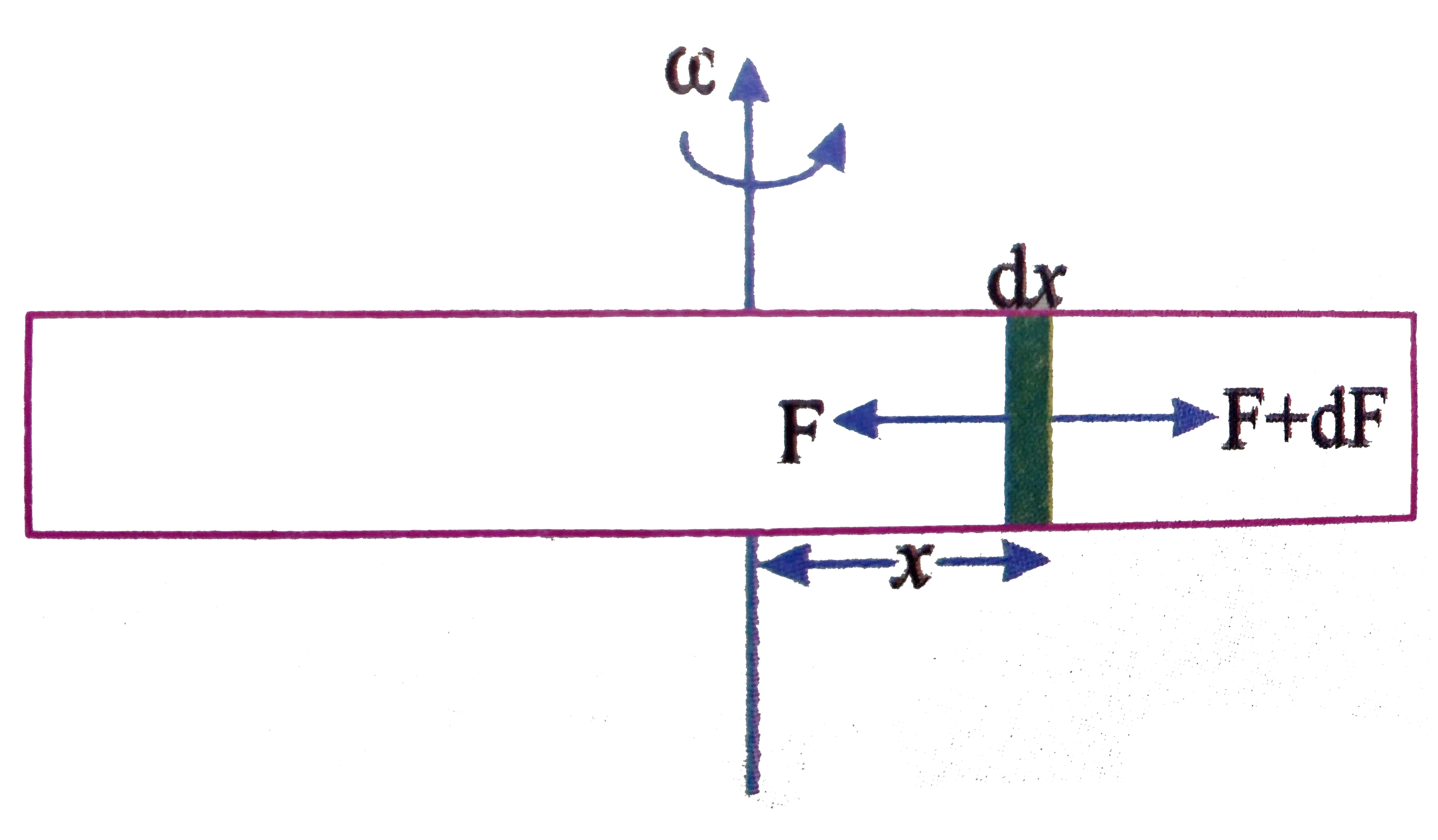 A1πl√2σmpBπl√2σmpC2πl√2σmpD3πl√2σmp
A1πl√2σmpBπl√2σmpC2πl√2σmpD3πl√2σmpA thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
Acentrifugal force acting on rod is mL2sinθω2 and will pass through centre of massBcentrifugal force acting on rod is mL2sinθω2 and will not pass through centre of massCθ=cos−1(3g2ω2L)Dθ=cos−1(gω2L)
A thin horizontal uniform rod AB of mass m and length l can rotate freely about a vertical axis passing through its end A. At a certain moment the end B starts experiencing a constant force F which is always perpendicular to the original position of the stationary rod and directed in a horizonatal plane. Find the angular velocity of the rod as a function of its rotation angle φ counted relative to the initial position.
View SolutionA smooth uniform rod AB of mass M and length l rotates freely with an angular velocity ω0 in a horizontal plane about a stationary vertical axis passing through its end A. A small sleeve of mass m starts sliding along the rod from the point A. Find the velocity v′ of the sleeve relative to the rod at the moment it reaches its other and B.
View SolutionA thin horizontal uniform rod AB of mass m and length l can rotate freely about a vertical axis passing through its end A. At a certain moment, the end B starts experiencing a constant force F which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. The angular velocity of the rod as a function of its rotation angle θ measured relative to the initial position should be.
View SolutionA rod AB of mass m and length l is rotating about a vertical axis as shown. It's moment of inertia about this axis is :
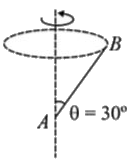
View SolutionA uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
View Solution
