A plane light wave with wavelength λ=0.50μm falls normally on the face of a glass wedge with an angle Θ=30∘. On the opposite face of the wedge a transparent diffraction grating with period, d=2.00μm is inscibed, whose lines are parallel to the wedge's edge. Find the angles that the direction of incident light froms with the directions to the principle Fraunhofer maxima of the zero and the first order. waht is the highest order of the spectrum? At what angle to the direction of incident light of the observed?
The diffraction formula is easily obtaind on taking account of the fact that the optical path in the glass wedge acquires a factor n(refractive index). We get
d(nsinΘ−sin(Θθk))=kλ
Isnce n>0,Θ−θ0>Θ and so θ0 must be nagative. we get, using Θ=30∘
32×12=sin(30∘−θ0)=sin48.6∘
Thus θ0=−18.6∘
Also for k=1
34−sin(30∘−θ+1)=λd=0.52.0=14
Thus θ+1=0∘
We calaculate θk for varoius k by the above fromula. For k=6.
sin(θk−30∘)=34⇒θk=78.6∘
For k=7
sin(θk−30∘)=+1⇒θk=120∘
This is in admissible. Thus the highest order that can be observed is
k=6
corresponding toθk=78.6∘
(for k=7 the diffracted ray will be grazing the wedge).

Similar Questions
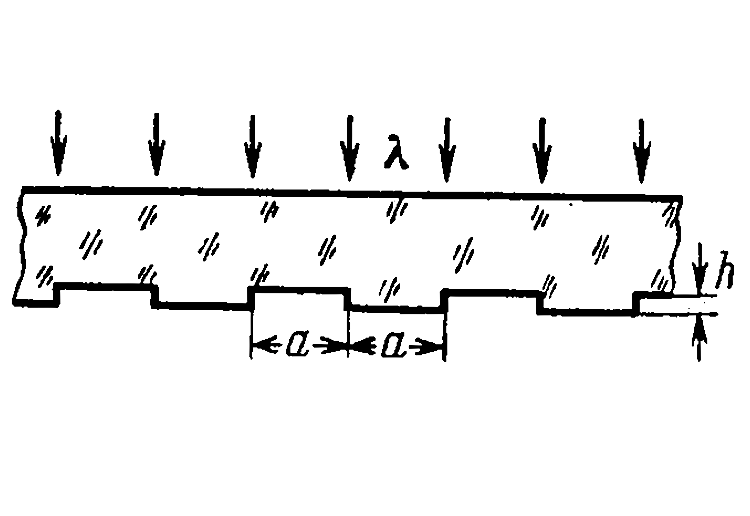
A plane light wave with wavelength λ falls normally on a phase diffraction grating whose side view is shown in Fig. The grating is cut on a glass plate with refractive index n. Find the depth h of the lines at which the intensity of the central Fraunhofer maximum is equal to zero. what is in this case the diffraction angle corresponding to the first maximum?
View SolutionA transparent diffraction grating has a period d=1.50μm. Find the angular disperison D (in angular minutes per nanometers) corresponding to the maximum of highest order for a spectral line of wavelength λ=530mm of light falling on the grating
(a) at right angles,
(b) at the angle θ0=45∘ to the normal.
View SolutionLight with wavelength lambda falls on a diffracting grating at right angles. Find the angular dispersion of the grating as a function of diffraction angle theta .
View SolutionLight with wavelength lambda = 589.0nm falls normally on a diffraction grating with period d = 2.5mu m , comprising N = 10 000 lines. Find the angular width of the diffraction maximum of second order.
View SolutionA beam of monochromatic light of wavelength λ falls normally on a diffraction grating of line spacing d. If θ is the angle between the second-order diffracted beam and the direction of the incident light, what is the value of sinθ ?
View SolutionA glass wedge of angle 0.01 radian is illuminated by monochromatic light of wavelength 6000 Å falling normally on it. At what distance from the wedge will 10th dark fringe be observed by reflected light ? (mu = 1.5) :
View SolutionA parallel bean of monochromatic light is allowed to incident normally on a plane transmission grating having 5000 lines per centimeter. A second order spectral line is found to be diffracted at an angle 30^(@) . Find the wavelength of the light. Data : N=5000 lines/cm =5000xx10^(2) lines/m, m=2 , theta=30^(@) , lambda=?
View Solution

