: To divide a line segment in a given ratio.
To divide a line segment in a given ratio, follow these step-by-step instructions:
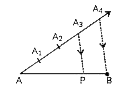
Step 1: Draw the Line Segment
- Draw a line segment AB of length 5 cm.
Step 2: Draw a Ray
- From point A, draw a ray AA' at any angle (not necessarily 90 degrees) to the line segment AB.
Step 3: Divide the Ray into Equal Parts
- Since the ratio given is 2:3, add the two parts of the ratio together (2 + 3 = 5).
- Use a compass to mark off equal segments on the ray AA'. Choose a convenient length for the compass and mark off 5 equal segments along the ray. Label these points as A1, A2, A3, A4, and A5.
Step 4: Join the Last Point to Point B
- Draw a line segment from point A5 to point B.
Step 5: Draw a Parallel Line
- Now, from point A2 on the ray, draw a line parallel to the line segment A5B. This parallel line will intersect the line segment AB at point P.
Step 6: Identify the Division Point
- The point P where the parallel line intersects AB is the point that divides the line segment AB in the ratio 2:3.
Conclusion
- You have successfully divided the line segment AB in the ratio 2:3.
---
- Draw a line segment AB of length 5 cm.
Step 2: Draw a Ray
- From point A, draw a ray AA' at any angle (not necessarily 90 degrees) to the line segment AB.
- Since the ratio given is 2:3, add the two parts of the ratio together (2 + 3 = 5).
- Use a compass to mark off equal segments on the ray AA'. Choose a convenient length for the compass and mark off 5 equal segments along the ray. Label these points as A1, A2, A3, A4, and A5.
- Draw a line segment from point A5 to point B.
- Now, from point A2 on the ray, draw a line parallel to the line segment A5B. This parallel line will intersect the line segment AB at point P.
- The point P where the parallel line intersects AB is the point that divides the line segment AB in the ratio 2:3.
- You have successfully divided the line segment AB in the ratio 2:3.
Similar Questions
Knowledge Check
If the extremities of a line segment of length l moves in two fixed perpendicular straight lines, then the locus of the point which divides this line segment in the ratio 1 : 2 is-
Aa parabolaBan ellipseCa hyperbolaDNone of these
Fill in the blanks/tables with suitable information:
In the given figure, P divides the line segment AB in the ratio ____________
View SolutionIn the given figure, ABCD is a parallelogram. AE divides the line segment BD in the ratio 1 : 2. If BE = 1.5 cm find BC.

View SolutionDivide a line segment AB in the ratio 3:7, What is the minimum number of points marked on a ray AX at equal distances?
View SolutionFind the point P divides the line segment joining the points (-1,2) and (4,-5) in the ratio 3:2
View SolutionPoint R (h, k) divides a line segment between the axes m the ratio 1:2. Find equation of the line.
View SolutionPoint P (h,k) divides a line segment between the exes in the ratio 1:2 Find the lengths (intercepts) on the axes made by this segment. Also find the area of triangle formed by the line segment and the axes.
View SolutionA line segment AB of length a moves with its ends on the axes.The locus of the point P which divides the segment in the ratio 1:2 is
View Solution
