एक त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि ∠ADC=∠BAC है दर्शाइए कि CA2=CB.CD है
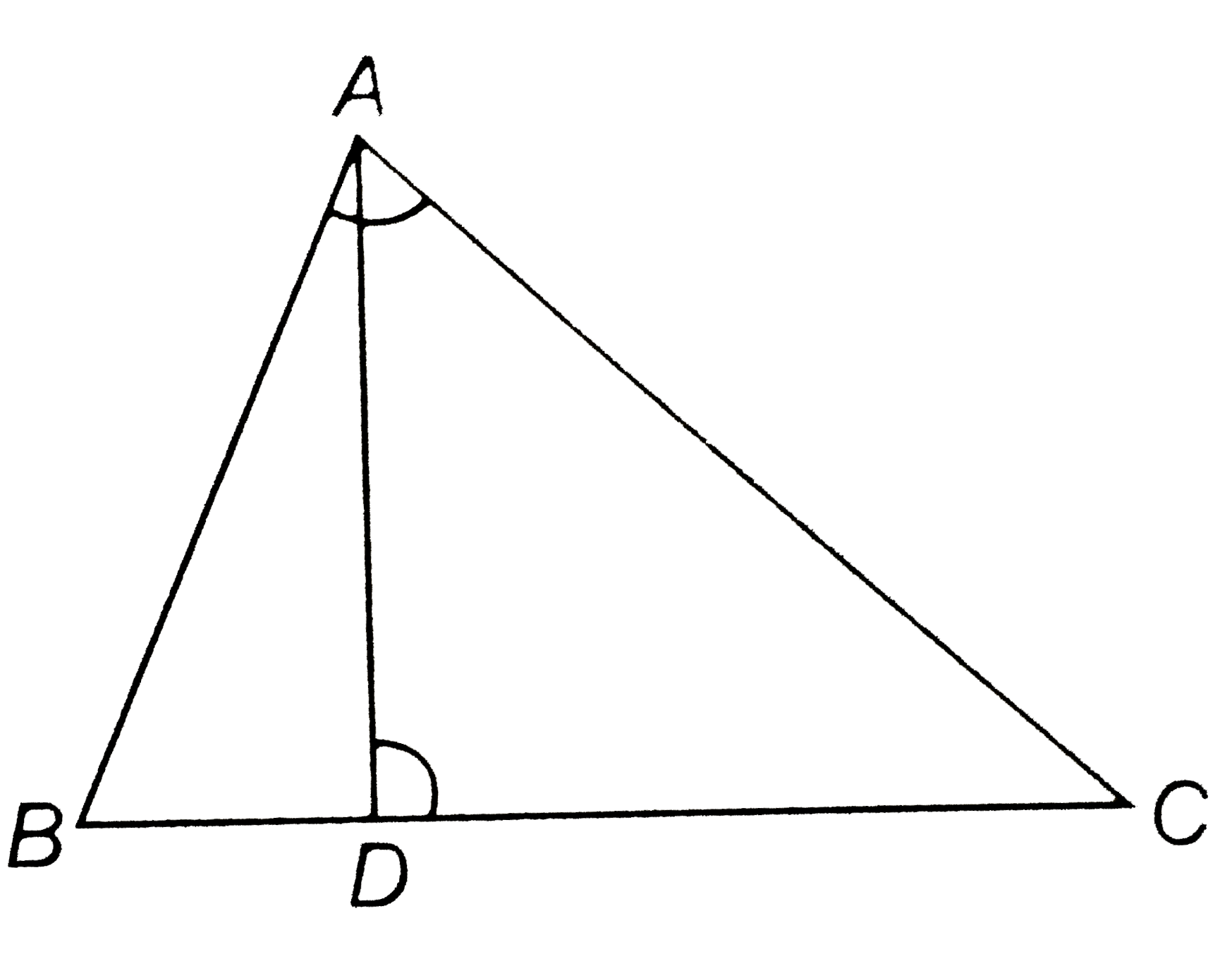
ΔABC और ΔDAC में
∠BAC=∠ADC (दिया है)
∠ACB=∠DCA (उभयनिष्ठ)
∴ ΔABC~ΔDAC (A.A समरूपता से)
⇒ CDCA=CACB
⇒ CA2=CB×CD यही सिद्ध करना था
Similar Questions
The inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
View SolutionIn the given fig. If DE||BC Find EC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/MATH_241_X_SQP_E01_021_Q01.png" width="80%"gt
View SolutionA and B are two points on a circle with centre O. AT is a tangent, such that angle BAT = 45^@ .N is a point on OA, such that BN= 10 cm. The length of the median OM of the triangle NOB is: A और B केंद्र O वाले एक वृत्त पर स्थित दो बिंदु हैं | AT एक स्पर्श रेखा है जो इस प्रकार है कि angle BAT = 45^@ है| N, OA पर स्थित एक बिंदु है जो इस प्रकार है कि BN =10 सेमी है | triangle NOB की मध्यिका OM की लंबाई ज्ञात करें |
View SolutionIn △ABC ,D is a point on side BC such that ∠ADC=∠BAC. If CA = 12 cm, and CB = 8cm, then CD is equal to :
त्रिभुज ABC में, D भुजा BC पर स्थित एक बिंदु है जो इस प्रकार है कि ∠ADC=∠BAC है |यदि CA = 12 सेमी और CB = 8 सेमी है, तो CD का मान किसके बराबर होगा ?
View Solution
