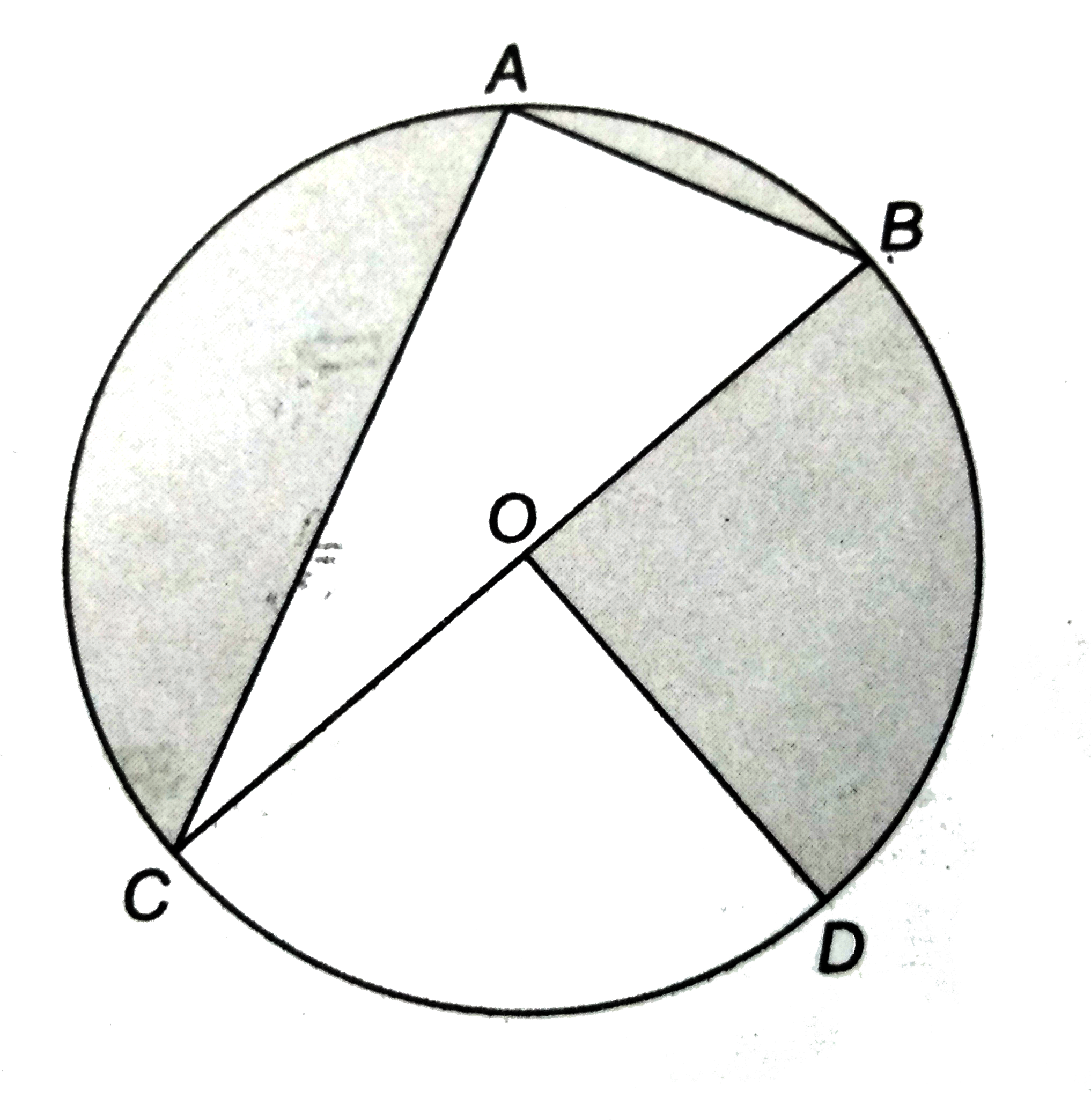
संलग्न आकृति में , O एक वृत्त का केंद्र है जिसमें AC = 24 सेमी ,AB = 7 सेमी और ∠BOD=90∘ है । छायांकित भाग का क्षेत्रफल ज्ञात कीजिए ।
Video Solution
Text Solution
∵O वृत्त का केंद्र है ,
∴BC वृत्त का व्यास है ।
∴∠CAB=90∘ (अर्द्धवृत्त में स्थित कोण समकोण होता है )
अब समकोण ΔACB में पाइथागोरस प्रमेय से
BC2=AC2+AB2=(24)2+(7)2=576+49=625
∴BC=√625=25 मीटर
∴ वृत्त का व्यास = 25 मीटर
∴ वृत्त की त्रिज्या = 252=12.5मीटर
∴OC=OD=12.5 मीटर ( प्रत्येक त्रिज्या )
∴ छायांकित भाग का क्षेत्रफल = वृत्त का क्षेत्रफल - ar(ΔABC)−ar (त्रिज्यखंड COD)
=π(12.5)2−12×AC×AB−π(OC)2×90∘360∘
=227×12.5×12.5−12×24×7−227×12.5×12.5×14
=491.07−84−122.768=284.302=284.30मीटर 2 (लगभग )
|
Similar Questions
The inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionIn the figure (not to scale) AB = AC and BD = CD. Find ∠ADB
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E05_003_Q01.png" width="80%"gt
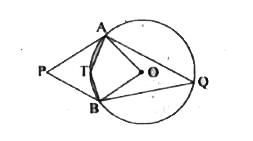
View Solutionआकृति में O वृत्त का केंद्र है। यदि ∠APB=70∘ तो ∠AQB का मान है -
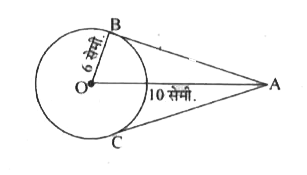
View Solutionदिये गये चित्र में O वृत्त का केंद्र है। AB व AC वृत्त कि स्पर्श रेखाएं है। यदि OA=10 सेमी तथा OB=6 सेमी है तो AC कि लम्बाई लिखिए।
View Solutionएक बेलन का व्यास 10 सेमी. तथा ऊंचाई 7 सेमी. है, तो बेलन का आयतन ज्ञात कीजिए।
View Solution
