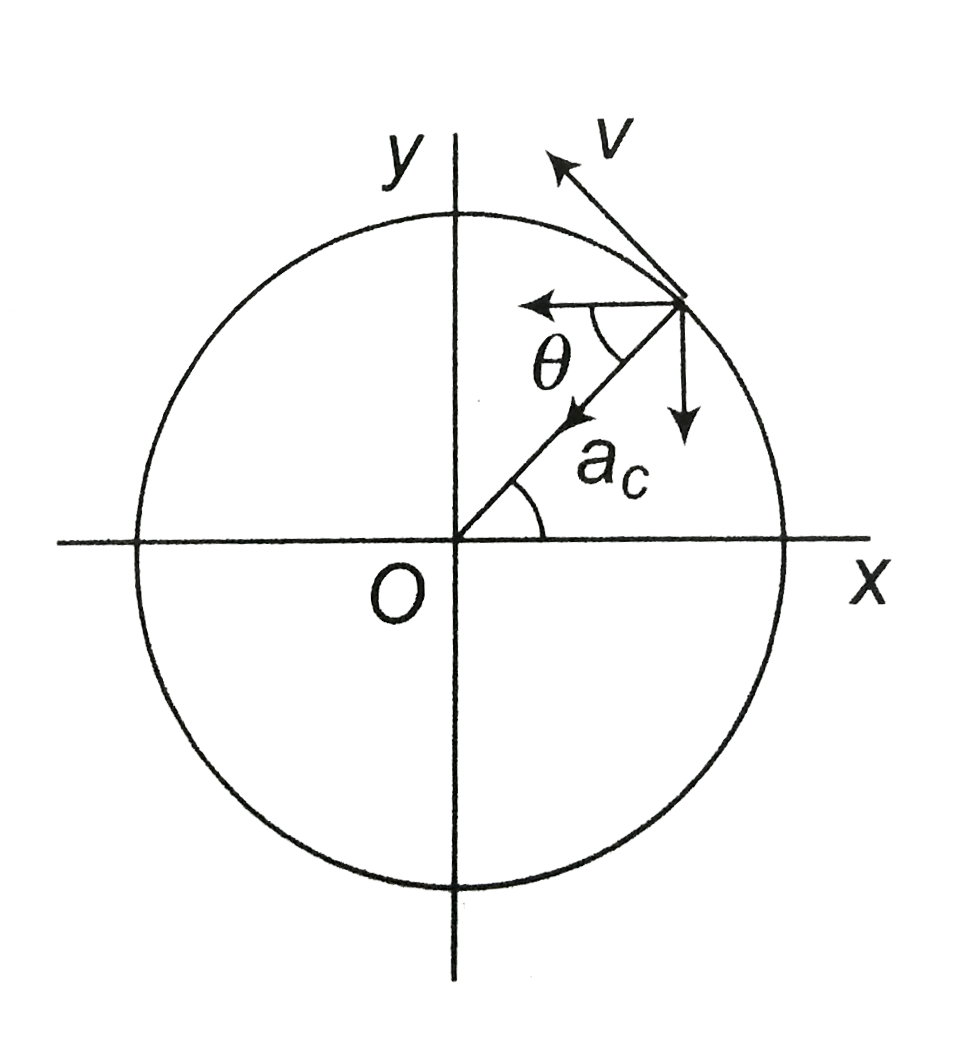
For a particle in uniform circular motion , the acceleration →a at a point p(R,θ) on the circle of radiu R is ( Here θ is measured from the x−aξs )
A
v2R→i+v2R→j
B
−v2Rcosθ→i+v2Rsinθ→j
C
−v2Rsinθ→i+v2Rcosθ→j
D
−v2Rcosθ→i−v2Rsinθ→j
Video Solution
Text Solution
The correct Answer is:D
→ac=accosθ(−ˆi)+acsinθ(−ˆj)
=−v2Rcosθˆi−v2Rsinθˆj
|
Similar Questions
Knowledge Check
For a particle in uniform circular motion the acceleration →a at a point P(R,θ) on the circle of radius R is : ( here θ is measured from the x- axis )
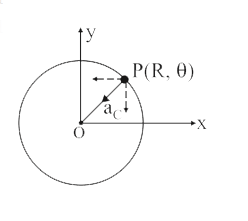 A−v2Rcosθˆi+v2RsinθˆjB−v2Rsinθˆi+v2RcosθˆjC−v2Rcosθhai−v2RsinθˆjDv2Rˆi+v2Rˆj
A−v2Rcosθˆi+v2RsinθˆjB−v2Rsinθˆi+v2RcosθˆjC−v2Rcosθhai−v2RsinθˆjDv2Rˆi+v2RˆjFor a particle performing a uniform circular motion the acceleration is
Aconstant in directionBconstant in magnitude but not in directionCconstant in magnitude and directionDconstant neither in magnitude nor in direction.In a non uniform circular motion, the acceleration on the particle is
Acentripetal acceleration onlyBtangential acceleration onlyCthe resultant centripetal and tangential accelerationDcentrifugal acceleration
Non-uniform circular motion: radial & tangential acceleration| Radius of curvature
View SolutionNon-uniform circular motion: radial & tangential acceleration| Radius of curvature
View SolutionFor a particle in a non-uniform accelerated circular motion
View SolutionThe area of a sector of angle θ∘ of a circle with radius R is
View SolutionA particle undergoes uniform circular motion. About which point on the plane of the circle, will the angular momentum of the particle remain conserved?
View Solution
