A ring of mass m and radius R is rolling down on a rough inclined plane of angle θ with horizontal. Plot the angular momentum of the ring about the point of contact of ring and the plane as a function of time
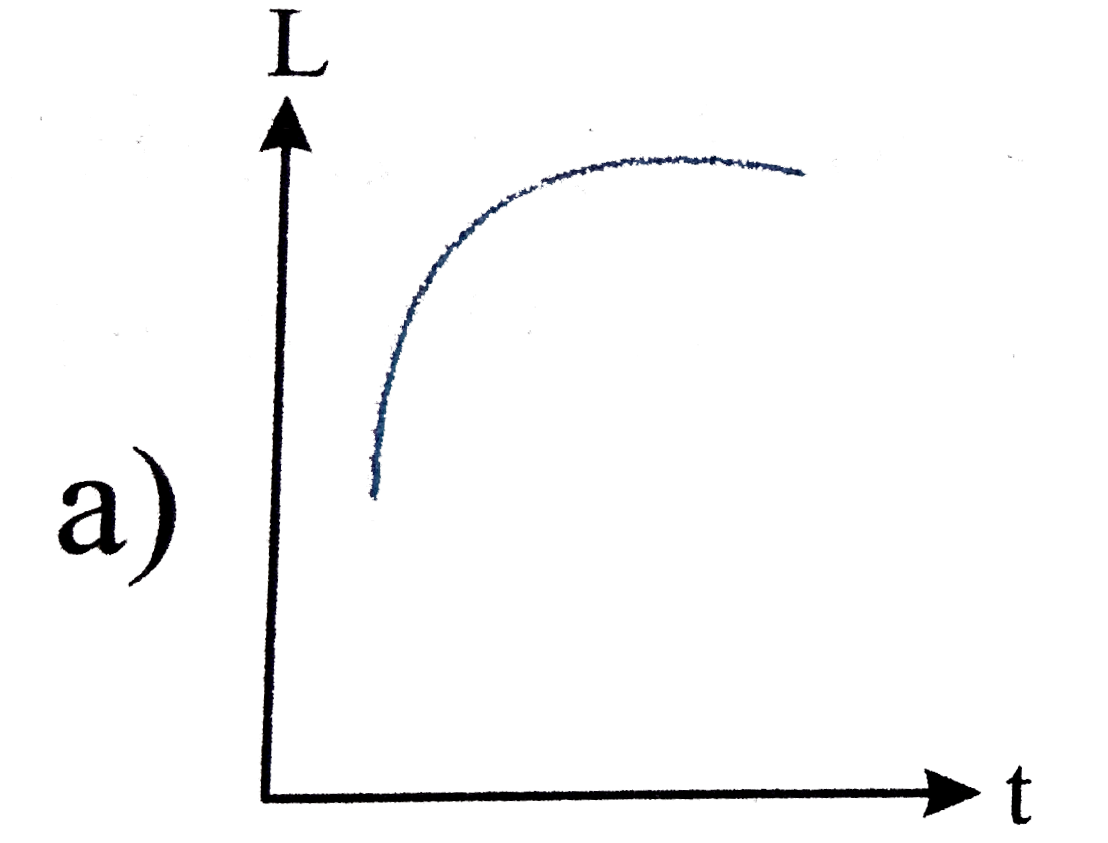


The correct Answer is:D
L=(mgsinθ)Rt, since , τ=ΔLΔt, so, L=τ(Δt)
The curve between L and time t will be a straight line.
Similar Questions
A ring is rolling down an inclined plane which is inclined at an angle of 30^(@) to the horizontal. Then the speed of ring after travelling a distance of 10 m is :-
View SolutionA cylinder and a ring of same mass M and radius R are placed on the top of a rough inclined plane of inclination theta . Both are released simultaneously from the same height h. When these bodies roll down to the foot of the inclined plane, then
View SolutionA ring of mass M is rolling down an inclined plane . The length of this plane is L . It makes an angle θ with the horizontal . Find the velocity of the centre of mass of the ring at the centre of the plane.
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v_0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA uniform ring of mass m and radius R is released from top of an inclined plane. The plane makes an angle theta with horizontal. The cofficent of friction between the ring and plane is mu . Initially, the point of contact of ring and plane is P. Angular momentum of ring about an axis passing from point P and perpendicular to plane of motion as a function of time t is
View SolutionA ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.



View SolutionFind the out the moment of inertia of a ring having uniform mass distribution of mass M and radius R about an axis which is tangent ot the ring and a in the plane of the ring b . perpendicular to the plane of the ring.
View SolutionA ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping. Match the following table.
View Solution
