A siphon has a uniform circular base of diameter 8/√πcm with its crest A,1.8m above the water level vessel B is of large cross section (g=10m/s2 and atmospheric pressure P0=105N/m2).
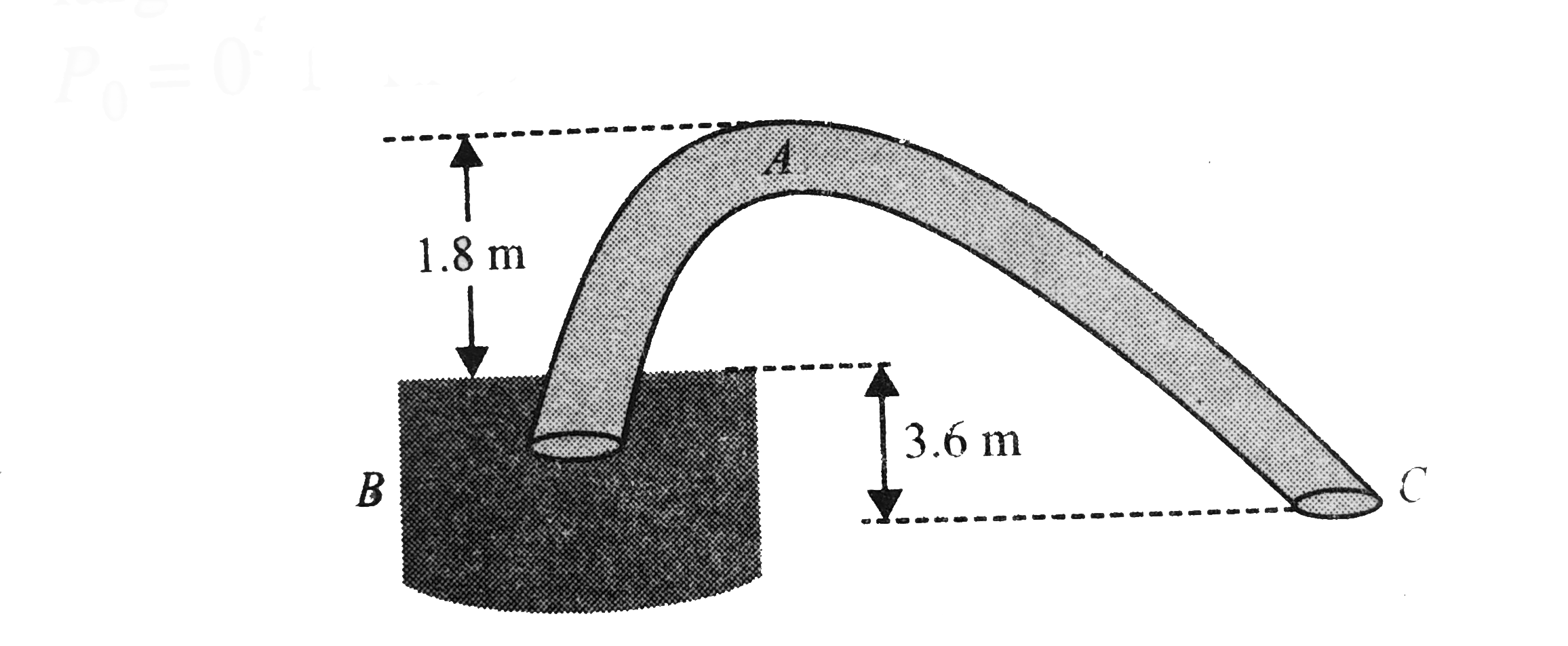
velocity of flow through pipe is 6√2m/s
Discharge rate of flow through pipe is 96√2×10−4m3/s
Velocity of flow through pipe is 6m/s
Pressure of A is 0.46×1−5N/m2
The correct Answer is:A, B, D

Applying bernoulli's equation at C and D, we have
P0+0+ρg(3.6)=P0+12ρv2+0⇒v=6√2m/s
Volume blown per unit time =av=πr2v=96√2
Similarly at A and C,
PA+12ρv2+ρg(3.6+1.8)=P0+12ρv2+0
PA=0.47×105N/m2
Similar Questions
The cross-sectional area of water pipe entering the basement is 4 x 10−4m2. The pressure at this point is 3 x 105Nm−2 and the speed of water is 2 ms−1. This pipe tapers to a cross-sectional area of 2 x 10−4m2 when it reaches the second floor 8 m above. Calculate the speed and pressure at the 2nd floor
View SolutionA capillary tube of diameter 0.20 mm is lowered vertically into water in a vessel. What should be the pressure in N//m^(2) to be applied on the water in the capillary tube so that water level in the tube is same as that in the vessel ? (surface tension of water is 0.07 N/m and atm pressure is 10^(5)N//m^(2))
View SolutionTen litre of water is compressed by an increase in pressure of 10 atmosphere. If the compressibility of water is 5xx10^(-10)m^(2)//N, then the change in volume of water will be (one atmosphere =10^(5)N//m^(2)).
View SolutionThe U-tube acts as a water siphon. The bend in the tube is 1m above the water surface. The tube outlet is 7m below the water surface. The water issues from the bottom of the siphon as a free jet at atmospheric pressure. Determine the speed of the free jet and the minimum absolute pressure of the water in the bend. Given atmospheric pressure =1.01xx 10^(5)N//m^(2),g=9.8 m//s^(2) and density of water =10^(3)kg//m^(3) .
View SolutionA glass capillary tube of inner diameter 0.28 mm is lowered vertically into water in a vessel. The pressure to be applied on the water in the capillary tube so that water level in the tube is same as the vessel in (N)/(m^(2)) is (surface tension of water =0.07(N)/(m) atmospheric pressure =10^(5)(N)/(m^(2))
View SolutionA tube of small uniform cross section is used to siphon the water from the vessel. Then choose the correct alternative (s) : (rho_("water") = 10^(3) kg//m^(3), g = 10 m//s^(2), P_(atm) = 10^(5) Pa)
View SolutionAt sea level, the atmospheric pressure is 1.04×105 Pa. Assuming g=10m s−2 and density of air to be uniform and equal to 1.3kg m−3, find the height of the atmosphere.
View SolutionA siphon has a uniform circular base of diameter 8/√πcm with its crest A,1.8m above the water level vessel B is of large cross section (g=10m/s2 and atmospheric pressure P0=105N/m2).

View Solution
