A string of negligible thickness is wrapped several times around a cylinder kept on a rough horizontal surface. A boy standing at a distance l from the cylinder holds one end of the string and pulls the cylinder toward him. Assuming no slipping the length of the thread passed through the hands of the man is

l2
l
2l
3l2
The correct Answer is:C
If velocity of centre of mass is v, then velocity of contact is 0 and that of the top is 2 v, hence when centre of mass covers a distance l, thread covers a distance 2l.

Similar Questions
A string of negligible thicknes is wrapped several times around a cylinder kept on a rough horizontal surface. A man standing at a distance l from the cylinder holds one end of the sitting an pulls the cylinder towards him figure. There is no slipping anywhere. The length of the string passed through the hand of the man whicle the cylinder reaches his hands is

View SolutionA string of negligible thickness is wrapped several times around a solid cylinder, which is kept on a rough inclined plane. A man exerts a force F through the string as shown in the figure and rolls without slipping the cylinder up through a vertical height h. The work done by the man is
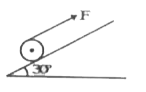
View Solution
Knowledge Check
A massless string is wrapped around a hollow cylinder having mass m and radius r. The cylinder is kept on a rough horizontal surface (coefficient of friction is μ). A constant force F is applied as shown in the figure. In case of pure rolling, the friction force acting on the bottom most point of the cylinder is
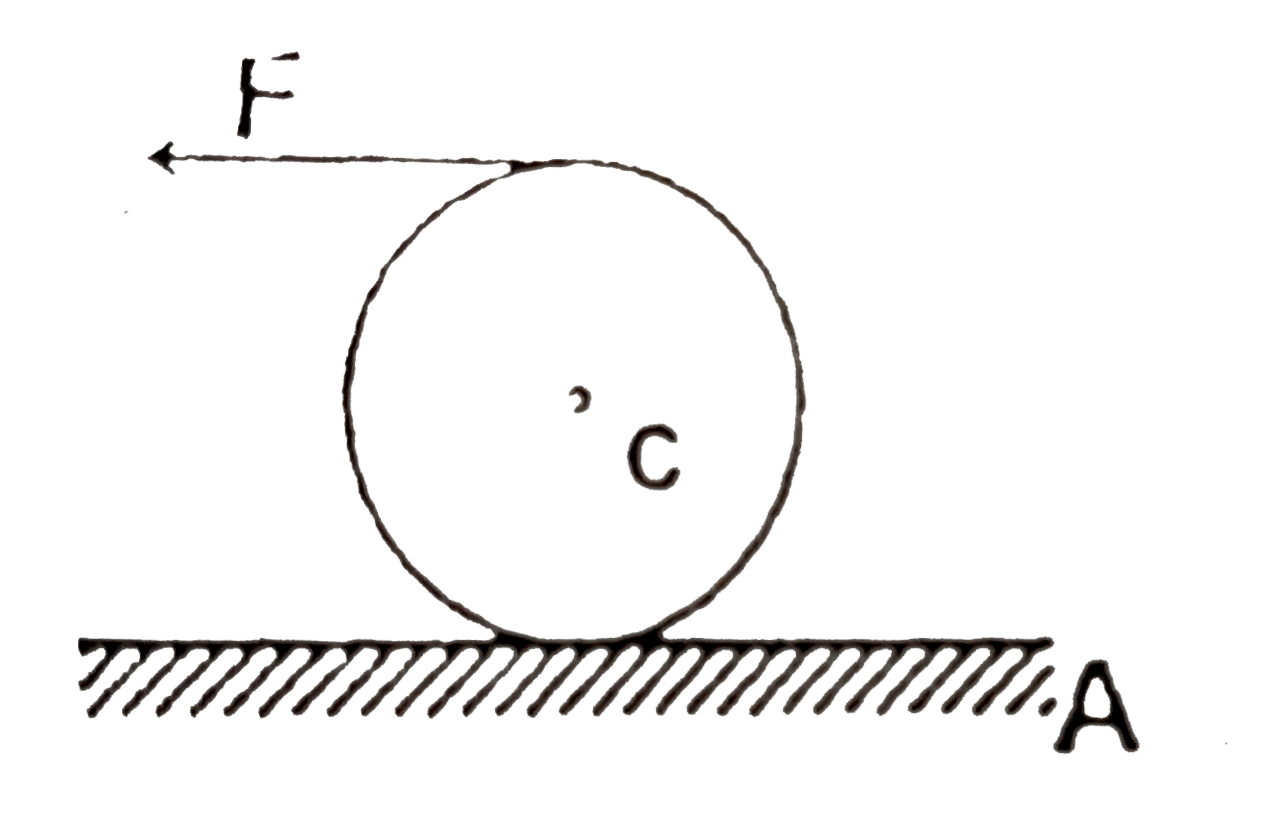 AzeroBμmgCμmg/2D3μmg/2
AzeroBμmgCμmg/2D3μmg/2A uniform solid cylinder of mass m and radius 2R rests on a horizontal table. A string attached to it passes over a pulley (disc) of mass m and radius R that is mounted on a fricitonaless axle through its centre . A block of mass m is suspended from the free end of the spring . The string does not slip over the pulley surface and the cylinder rolls without slipping on the table.
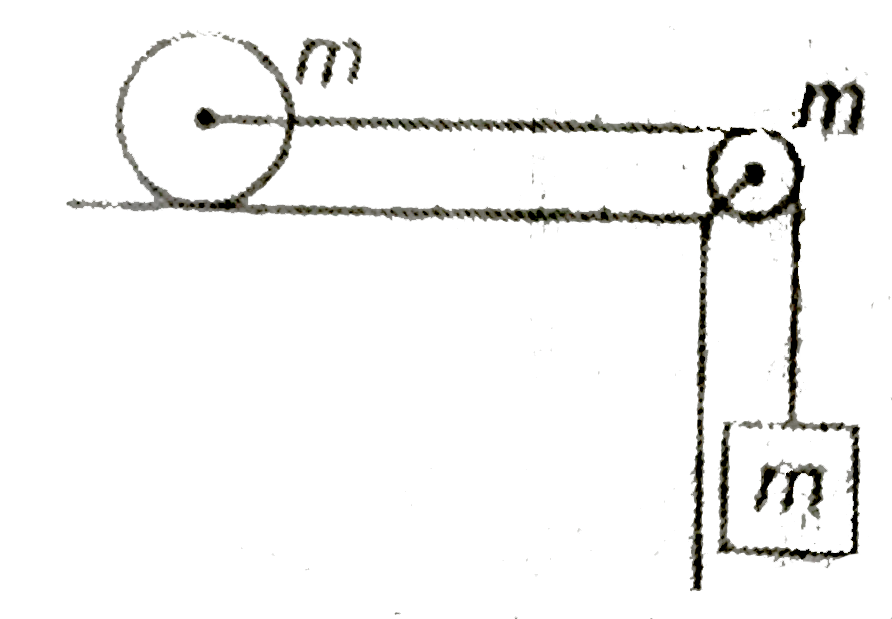
Angular acceleration of the cylinder isAg3RB3g2RCg6RDg9R
There is a tall cylindrical building standing in a field. Radius of the cylinder is R=8m. A boy standing at A (at a distance of 10 m from the centre of the cylindrical base of the building) knows that his friend is standing at B behind the building. The line joining A and B passes through the centre of the base of the building. Distance between A and B is 50 m. A wants to throw a ball to B but he realizes that the building is too tall and he cannot throw the ball over it. He throws the ball at a speed of 20m/s such that his friend at B has to move minimum distance to catch it.

(a) What is the minimum distance that boy at B will have to move to catch the ball?
(b) At what angle to the horizontal does the boy at A throws the ball? Assume that the ball is released and caught at same height above the ground.
[Take g=10m/s2 and sin−1(0.75)≅48.6∘
View SolutionA solid cylinder has a thin string wrapped several times around its circumference. The string is fixed at one end and the cylinder is released. Find the downward acceleration of cylinder and tension in the string.
View SolutionA string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upward to prevent the centre of mass from falling as the string unwinds. Assume that the cylinder remains horizontal throughout and the thread does not slip. Find the length of the string unwound when the cylinder has reached an angular speed ω.
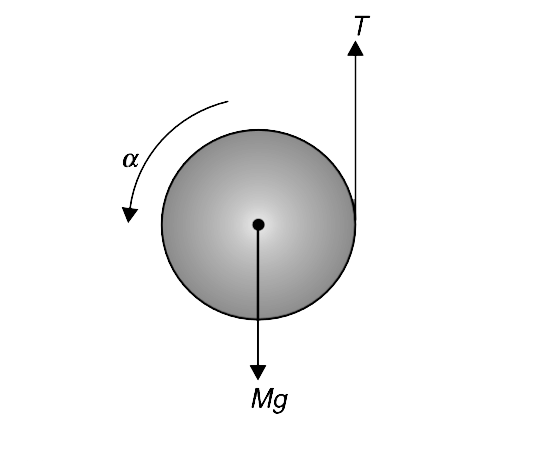
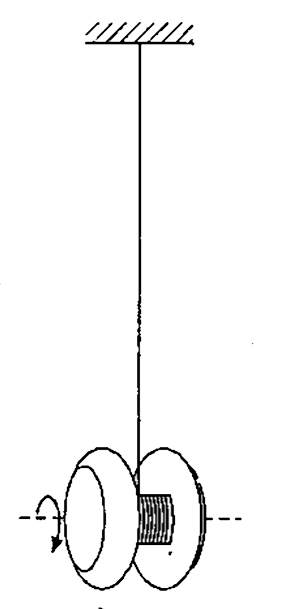
View SolutionA primitive yo-yo is made by wrapping a string several times around a solid cylinder with mass M and radius R shown in figure-5.56. The end of the string stationary while releasing the cylinder with no initial motion. The string unwinds but does not slip or Stretch as the cylinder drops and rotates. Use energy considerations to find the speedv ofthe centre ofmass ofthe solid cylinder after it has dropped a distance h.
View SolutionA large mass M and a small mass m hang at the two ends of string passing through a smooth tube. The mass m moves around in a circular path in a horizontal plane. The length of the string from the mass m to the top of the tube of the tube is l and θ is the angle this length makes with the vertical. What should be the frequency of rotation of the mass m so that M remains stationary ?
View SolutionA string is wrapped around a cylinder of mass M and radius R(=2√2m).The string is pulled vertically upward to prevent the centre of mass from falling as the cylinder unwinds the string.Find the length of the string unwound when the cylinder has reached a speed ω(=5rad/s).(g=10ms2)
View Solution

