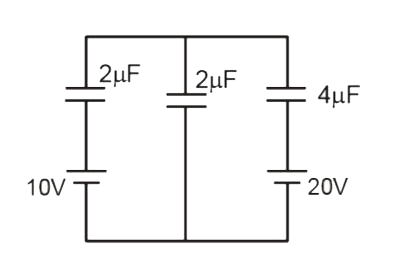
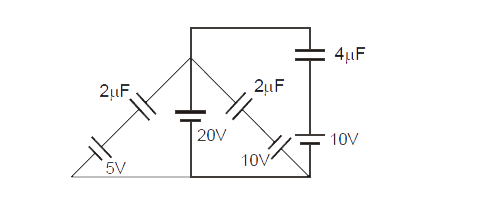
(a) Find charge on capacitors

(b) Find charge on capacitor
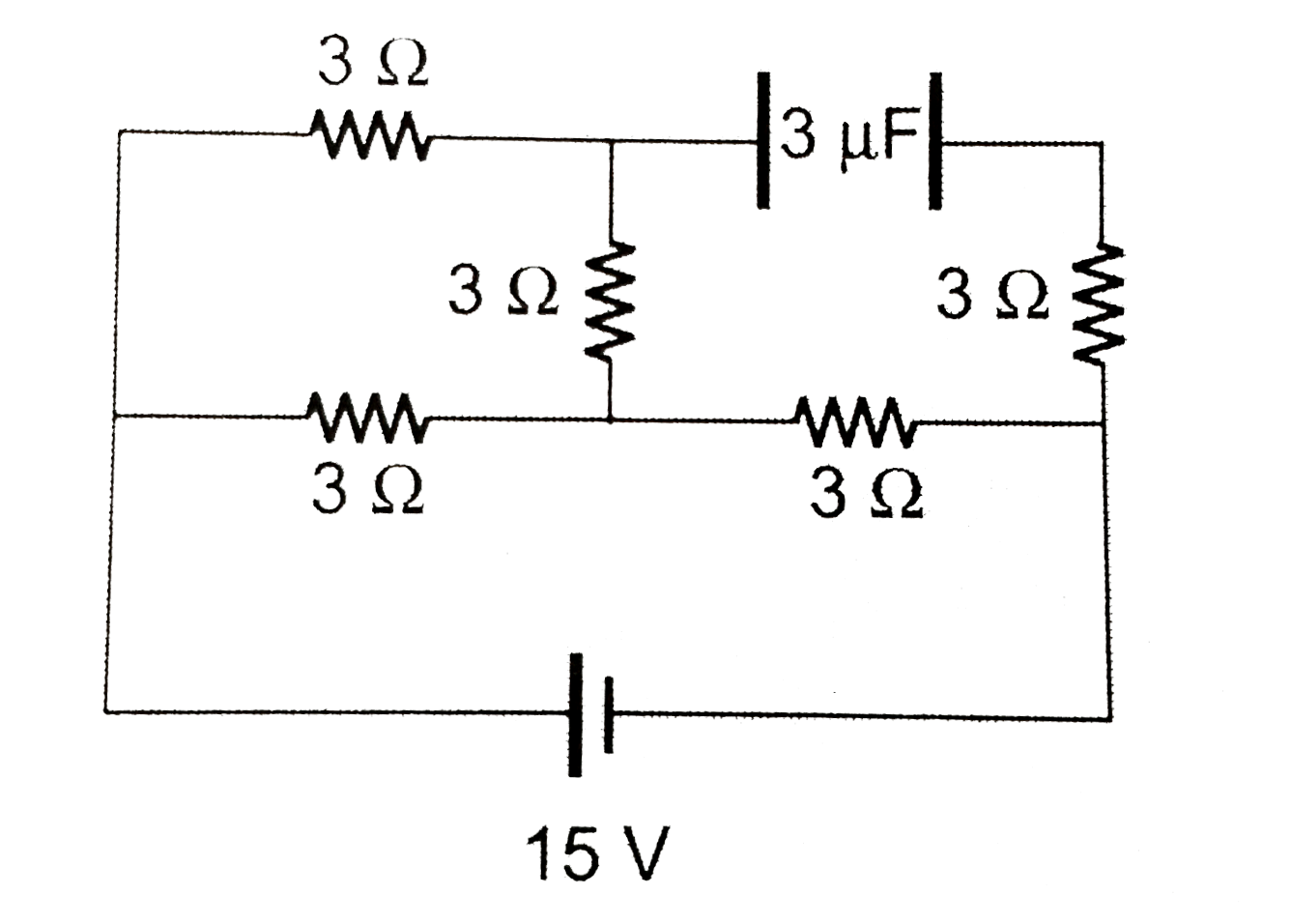
(c ) Find energy stored in capacitor.
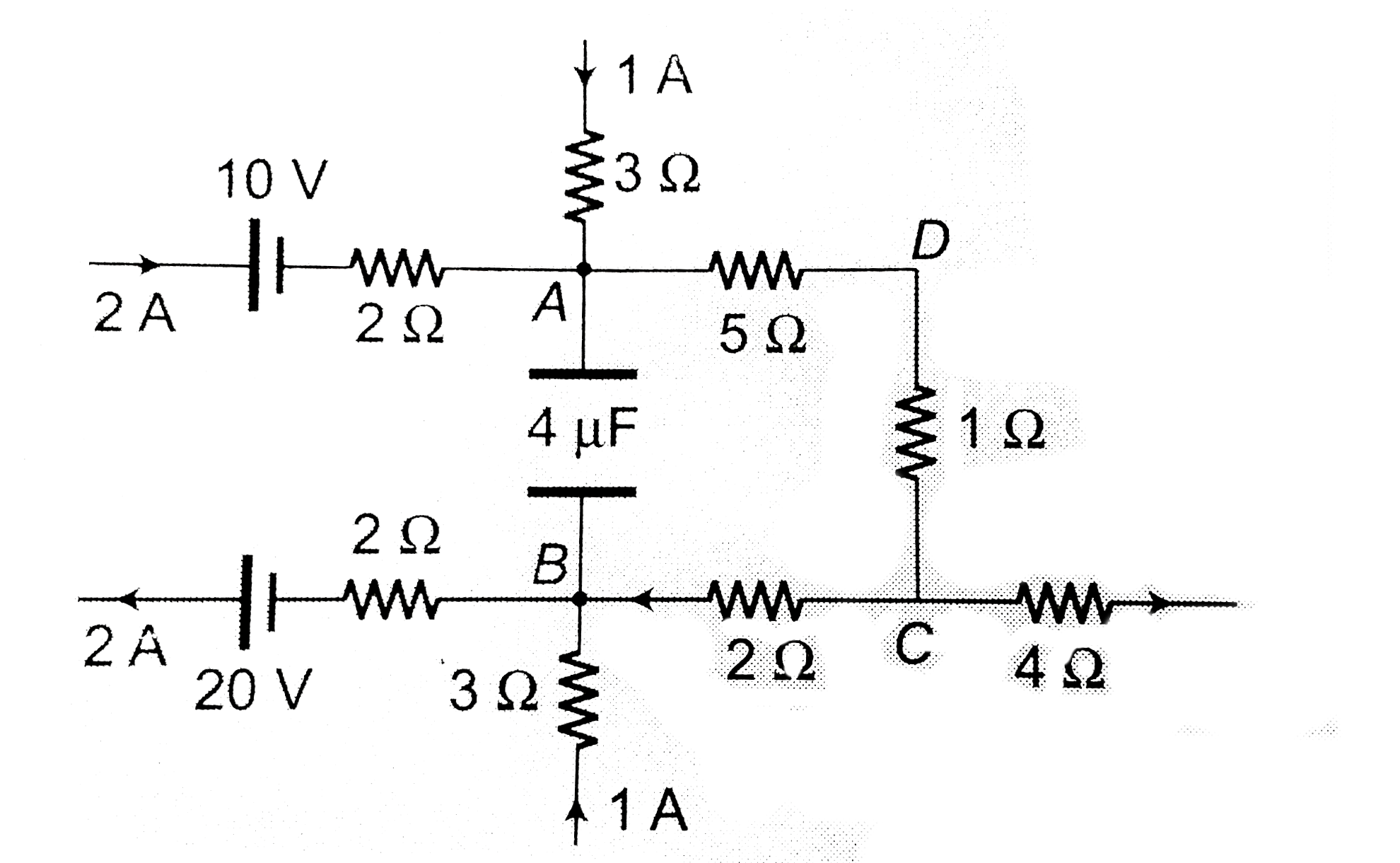
Video Solution
Text Solution
(a) 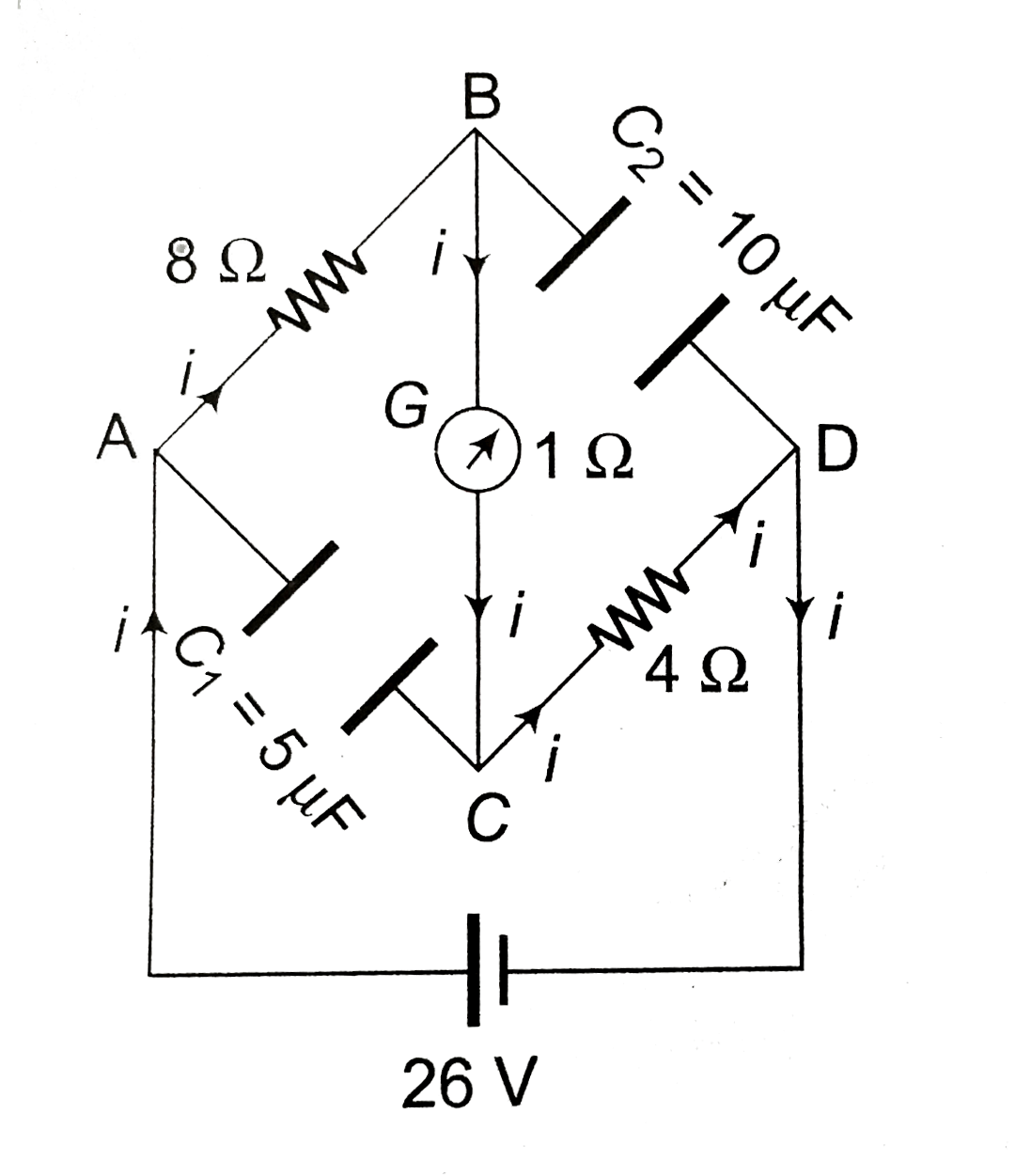
Req=8+1+4=13Ω
i=2613=2A
VA=i×8−i×1=VC
VA−VC=9i=9×2=18V
Charge on C1 :
Q1=C1(VA−VC)=5×18=90μC
VB=i×1−i×4=VD
V_(B)-V_D=5i=5xx2 = 10V<br>Char≥onC_(2):<br>Q_(2) - C_(2) (V_(B)-V_(D)) = 10xx10 = 100muC<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/CPS_V02_C04_S01_025_S02.pngwh=80%mx-autosty≤=background:white;margin-top:12px;margin-bottom:12px;><br>BetweenAandO,viaX , 3Omegaand3Omegaare∈seriesie.,6 Omega.<br>BetweenAandO,6Omega and 3Omegaare∈paral≤lie.<br>(6xx3)/(6+3_ = 2 Omega<br>R_(eq)=2+3 = 5Omega<br>i=15/5 = 3A<br>i_(1) = 3/(3+6)xxi = 1A<br>i=i_(1)=3-1=2A<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/CPS_V02_C04_S01_025_S03.pngwh=80%mx-autosty≤=background:white;margin-top:12px;margin-bottom:12px;><br>V_(X)-1xx3-3xx3=V_(Y) implies V_(X)-V_(Y) = 12V<br>Char≥on∩aci→rQ = C(V_(X)-V_Y)<br>=3xx12=36muC<br>(c)Firstdeterminedcurrents∈thebranches<br>ADCandCBbyjunctionlawatjunctionsA and B.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/CPS_V02_C04_S01_025_S04.pngwh=80%mx-autosty≤=background:white;margin-top:12px;margin-bottom:12px;><br>V_(A) -3xx5-3xx1-1xx2=V_(B)<br>V_(A)-V_(B)=V= 20V<br>p.d.across∩ai→rV = 20V<br>theenregys→red∈∩acior<br>U - 1/2 CV^2<br>=1/2 xx 4xx10^(-6)xx(20)^(2)<br>=400xx10^(-6)J<br>=400muJ.
|
Similar Questions
Knowledge Check
Find out total energy stored in the capacitors.
A500μJB300μJC600μJD1300μJ
Find charge on each capacitor.
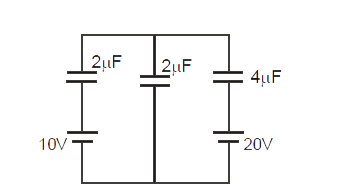
View SolutionFind charge in each capacitor:
View SolutionFind charge in each capacitor:
View SolutionFind the charge stored in the capacitor.
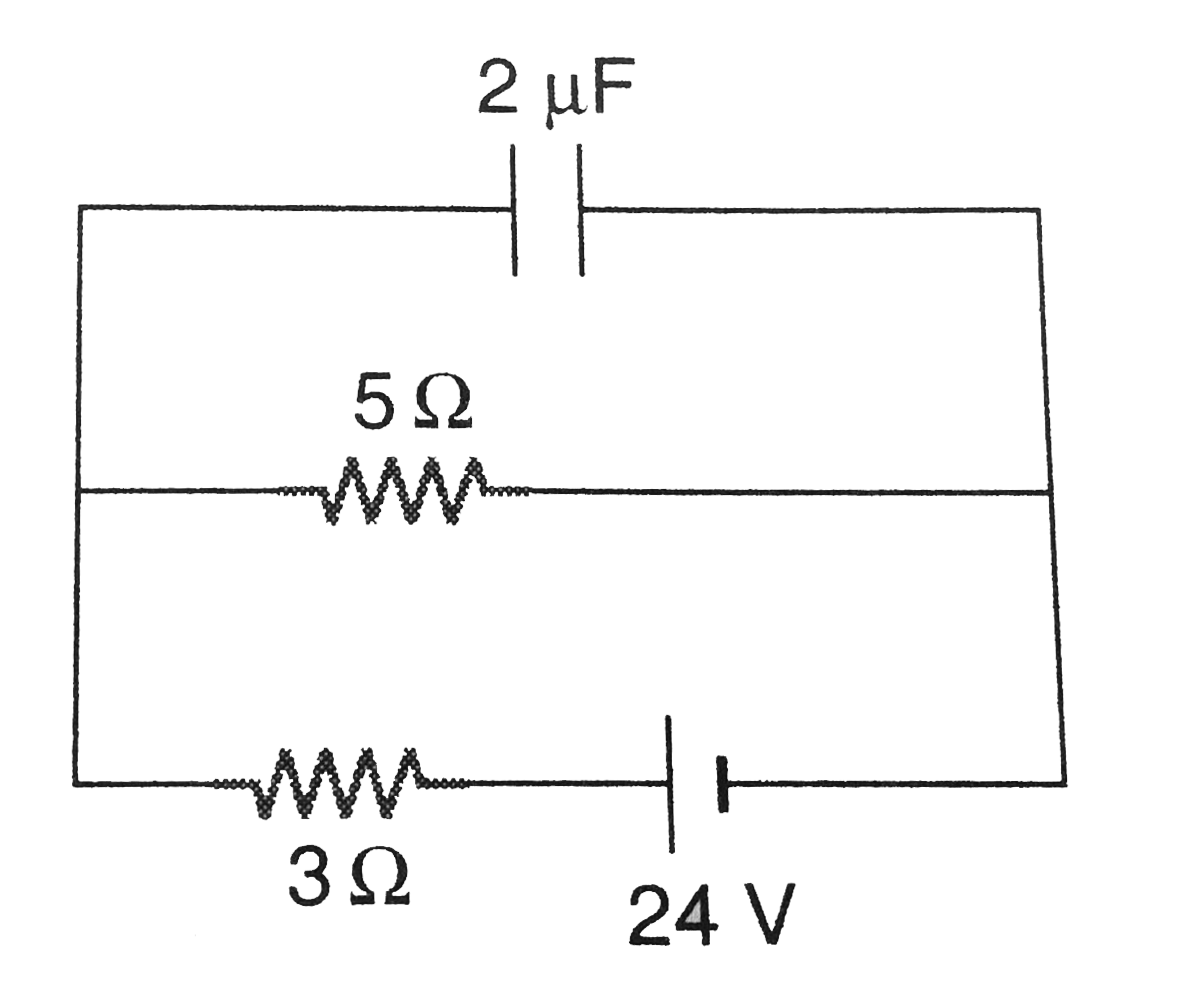
View SolutionFind the charge stored in the capacitor.
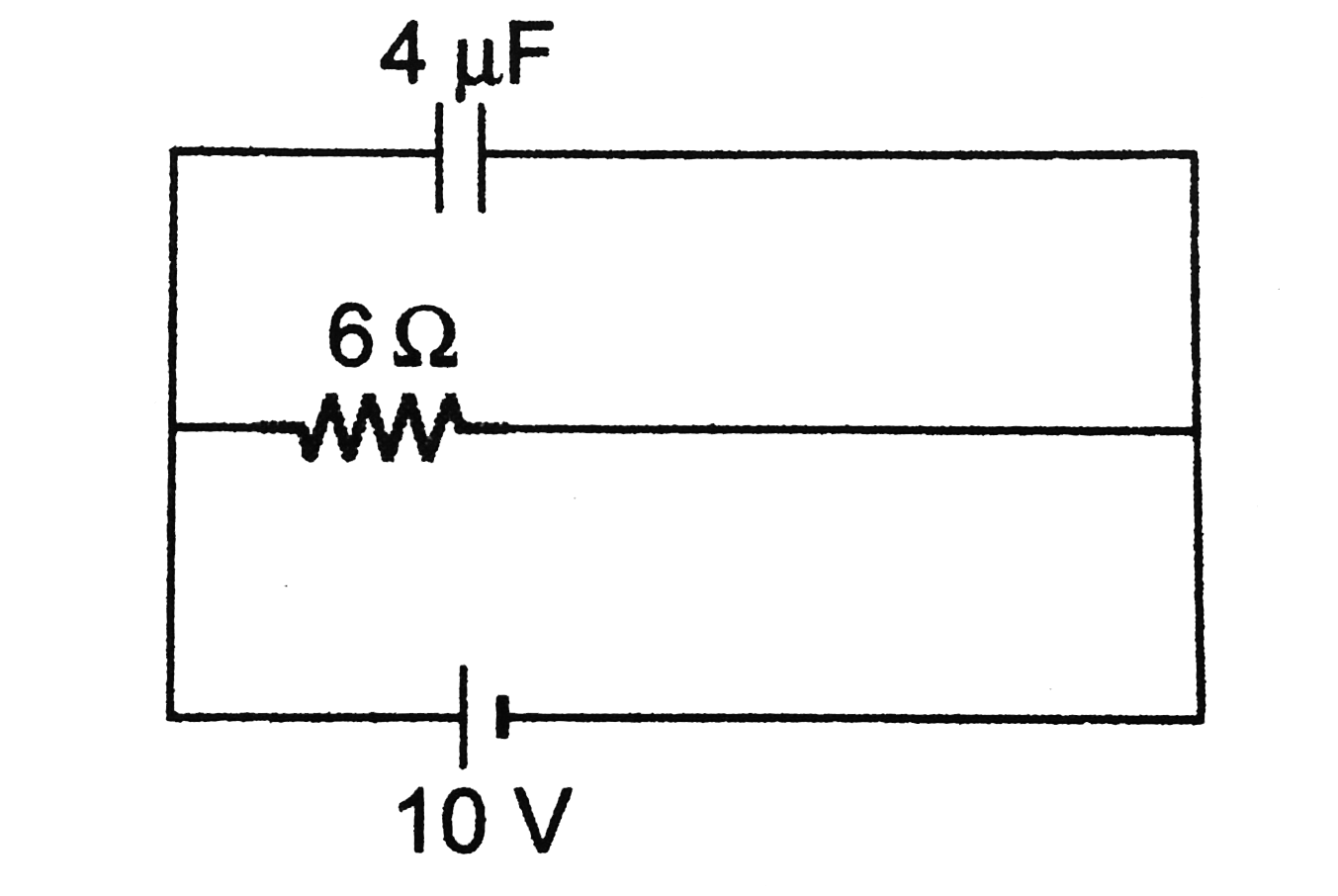
View SolutionFind the charge stored in the capacitor.
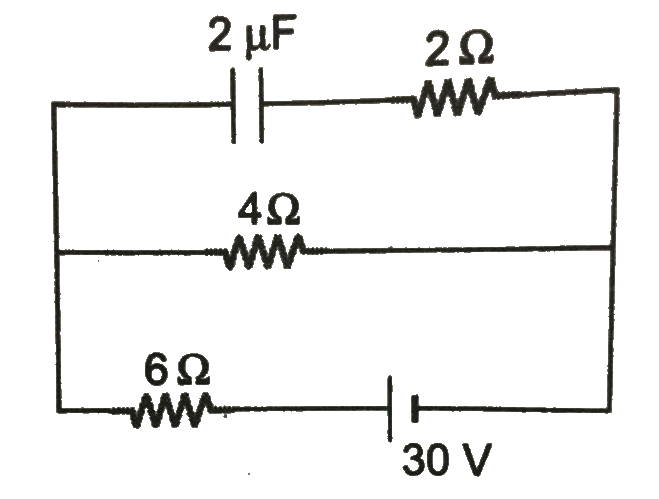
View SolutionFind the charge on capacitor in steady state.
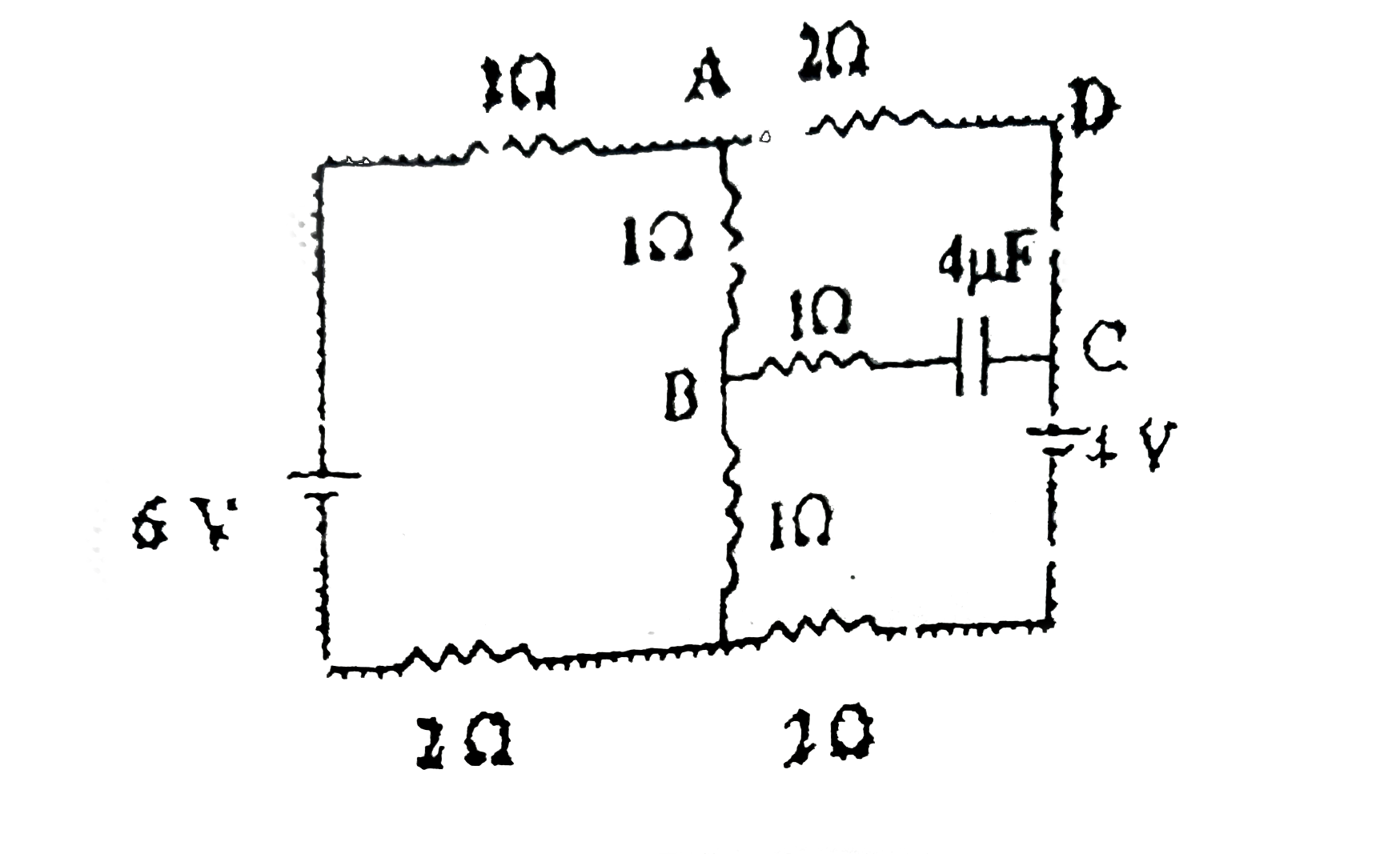
View Solution