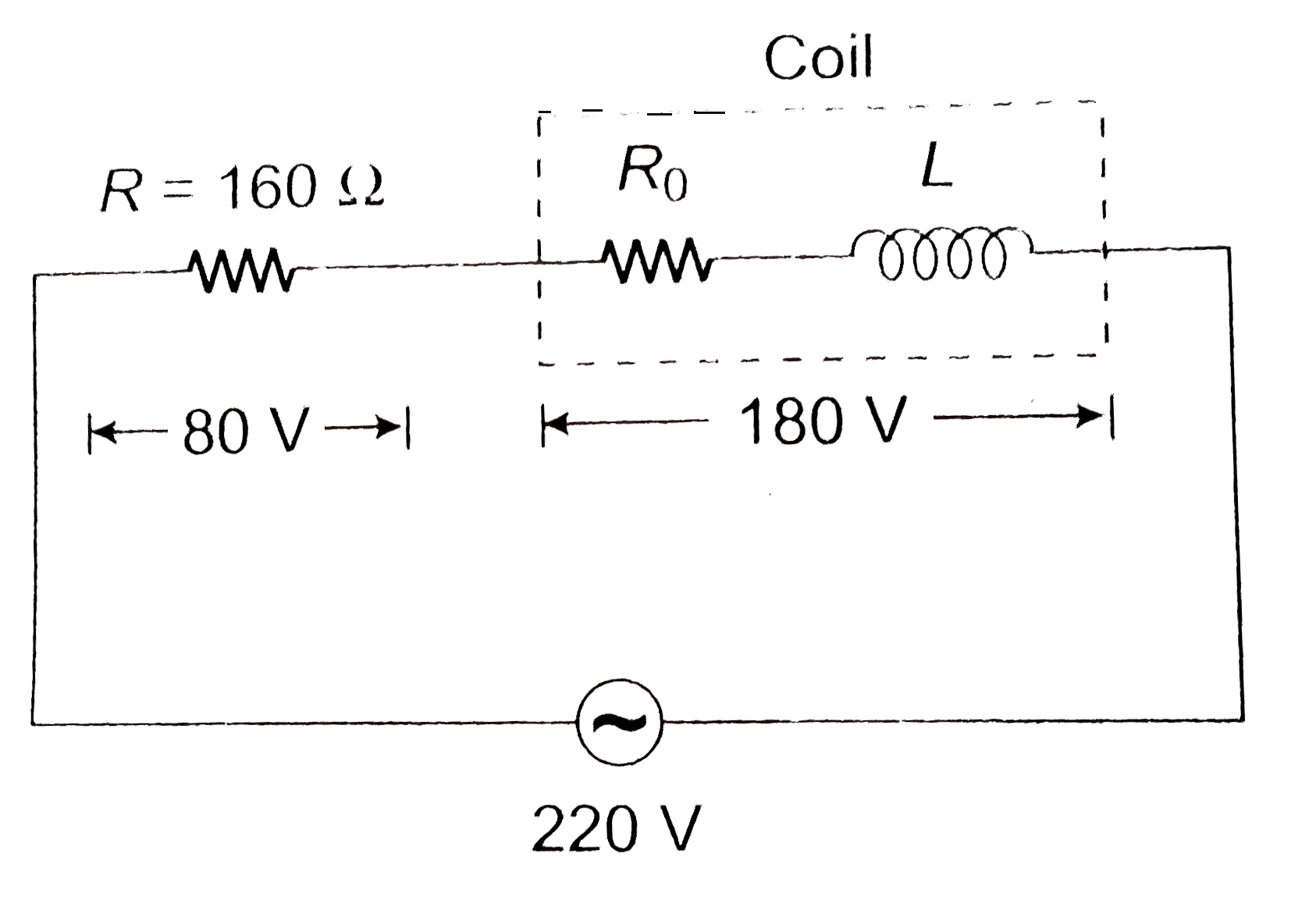
A series circuit consisting of an inductance free resistance R=0.16kΩ and a coil with active resistance is connected to the mains effective voltage V=220V Find the heat power generated in the coil if the effective voltage values across the resistance R an the coil equal to V1=80V and V_(2) =180V respectively .
Current in the circuit
VR=irmsR
80=Irms×160⇒irms=12A
VRo=irmsR0=R02
VL=irmsXL=XL2
(VR+VR0)2+V2L=(200)2
(80+R02)2+(XL2)2=(200)2−(1800)2
(80+R0)(80)=(400)(40)
Power consumed in coil
P=i2rmsR0=(12)2×120=30W
 .
.
Similar Questions
A series circuit consisting of an inductance − free resistance R=0.16kΩ and coil with active resistance is connected to the mains with effective voltabe V=220V. Find the heat power generated in the coil if the effective voltage values across the resistance R and the coil are equal to V1=80V and V2=180V respectively.
View SolutionA coil with inductive resistance XL=30Ω and impedance Z=50Ω is connected to the mains with effective oltage value V=100V. Find the phase difference between the current and the voltage, as well as the heat power generated in the coil.
View Solution
Knowledge Check
A coil of inductance 5.0 mH and negligible resistance is connected to an alternating voltage V=10sin(100t). The peak current in the circuit will be:
A2 ampB1 ampC10 ampD20 ampA coil of inductance 5.0 mH and negligible resistance is connected to an alternating voltage V=10sin(100t). The peak current in the circuit will be:
A2ampB1ampC10ampD20ampA 20volts AC is applied to a circuit consisting of a resistance and a coil with negligible resistance. If the voltage across the resistance is 12V, the voltage across the coil is
A16 voltsB10 voltsC8 voltsD6 volts
A coil with inductive reactance XL=30Ω and impedance Z=50Ω is connected to the mains with effective voltage value V=100V Find the phase difference between the current and voltage as well as the heat power generated in the coil .
View SolutionA coil with active resistance R and inductance L was connected at the moment t=0 to a source of voltage V=Vmcosωt. Find the current in the coil as a function of time t.
View SolutionA coil and an inductance − free resistance R=25Ω are connected in parallel to the ac1 mains. Find the heat power generated in the coil provided a current I=0.90A is drawn from the mains. The coil and the resistance R carry currents I1=0.50A and I2=0.60A respectively.
View SolutionA circuit consists of a capacitor with capacitance C and a coil with active resistance R and inductance L connected in parallel. Find the impedane of the circuit at frequency ω of alternating voltage.
View SolutionA coil of inductance 1H and neligible resistance is connected to a source of supply, whose voltage is given by V=4VOLT. If the voltage is applied at t=0, find the energy stored in the coil in 4s
View Solution

