Two identical balls (A) and (B) each of mass (0.1 kg), are attached to two identical massless springs. The spring - mass system is constrained to move inside a riged smooth pipe bant in the form of a circle as shown in Fig. The pipe is fixed in a horizontal plane.
The centres of the balls can move in a circle of radius (0.06 pi) meter. Each spring has a natural length zof0.06π meter and spring spring constant5 0.1N/m. Initially, both the balls are displaced by an angle θ=π/6 radian with respect to the diameter (pQ) of the circle (as shown in Fig.) and released from, rest.
 .
.
(i) Calculate the frequency of oscillation of ball (B).
(ii) Find the speed of ball (A) when (A) and (B) are at the two ends of the diameter (PQ).
(iii) What is the total energy of the system.
3.9×10−4J
10−4J
6×10−4J
2×10−4J
The correct Answer is:A
Given-Mass of each block A and b,m=0.1kg Radius of circle, R=0.06m

Natural length of spring l0=0.06π=πR (Half circle) and spring constant, k=0.1N/m In the streteched position elongation in each spring x=Rθ. Let us draw FBD of A
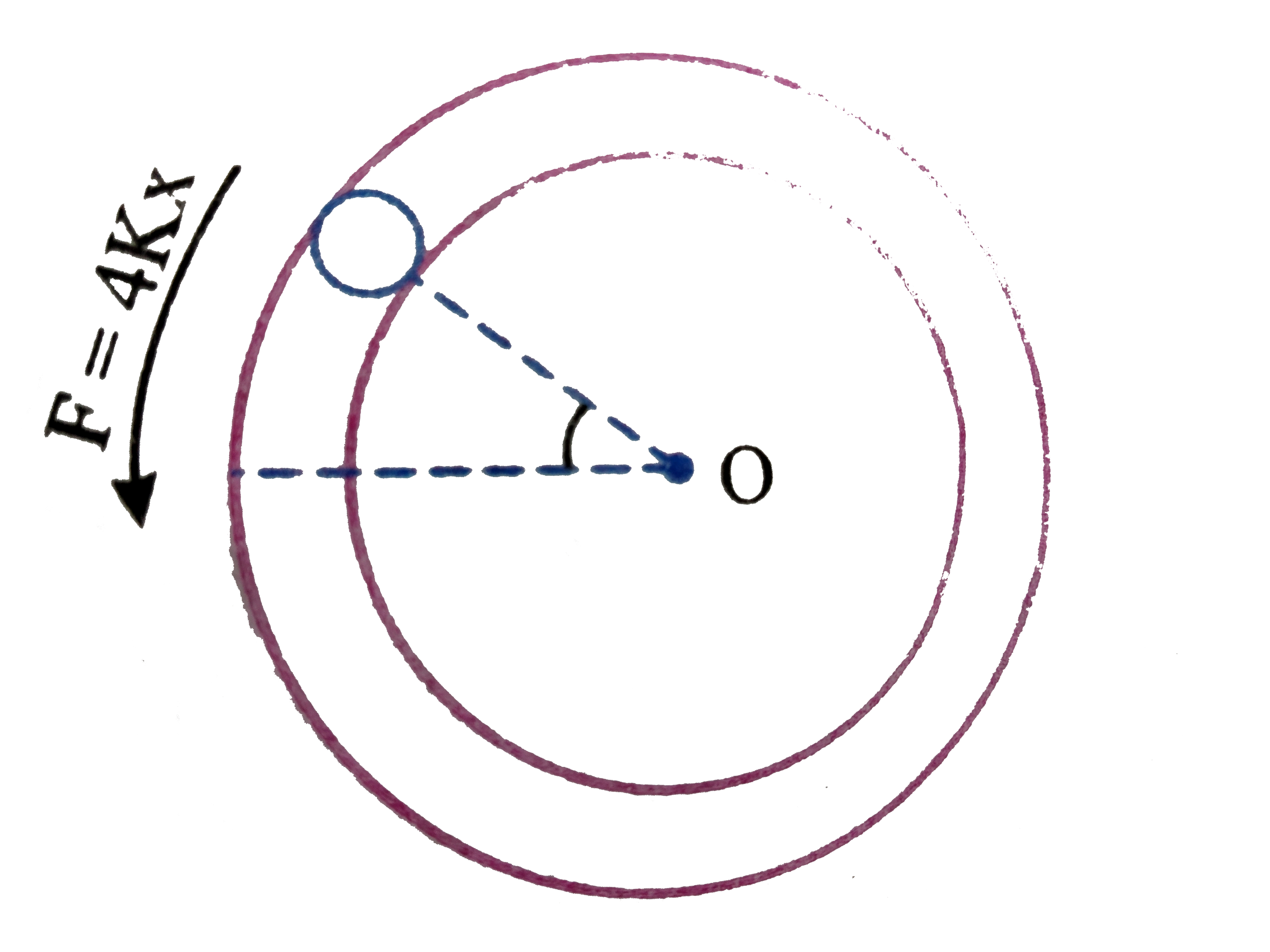
Spring in lower side is stretched by 2x and on upper side compressed by 2x. Therefore, each spring will exert a force 2kx on each block. Hence, a restroing force, F=5kx will acr on A in the direction shown in figure.
tai=−F.R=−(4kx)R=−(4kRθ)Rorτ=−4kR2.θ(1)
Since, each ball executes angular SHM about origin O. Eq. (1) can be rewritten as
Iα=−4kR2qor(mR2)α=−4kR2θorα=−(4km)θ
∴ Frequency oscillation, f=12π√∣∣∣accelerationdisplacement∣∣∣=12π√∣∣∣αθ∣∣∣
f=12π√4km Substituting the values, we hae
f=12π√4×0.10.1=1πHz
(ii) In stretched position, potential energy of the system is PE=2{12k}{2x}2=4kx2 and in mean position, both the blocks have kinetic enegry only.
Hence, KE=2{12mv2}=mv2 From energy conservation
PE=KE,∴4kx2=mv2
∴v=2x√km=2Rθ√km
∴v=2(0.06)(π6)√0.10.1orv=0.0628m/s
(iii) Total energy of the sysetm, E=PE in stretched position or =KE in mean position
E=mv2=(0.1)(0.0628)2JorE=3.9×10−4J
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage-II
Explore 2 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage-III
Explore 2 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage-I
Explore 2 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
For SHM to take place force acting on the body should be proportional to −x or F=−kx. If A be the amplitude then energy of oscillation is 1/2KA2.
Force acting on a block is F=(−4x+8). Here F is in newton and x in the position of block on x-axis in meters
View SolutionA circular tube of uniform cross section is filled with two liquids densities ρ1 and ρ2 such that half of each liquid occupies a quarter to volume of the tube. If the line joining the free surfaces of the liquid makes an angle θ with horizontal find the value of θ.

View SolutionTwo identical blocks P and Q have mass m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by A/2 and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both the blocks was T.
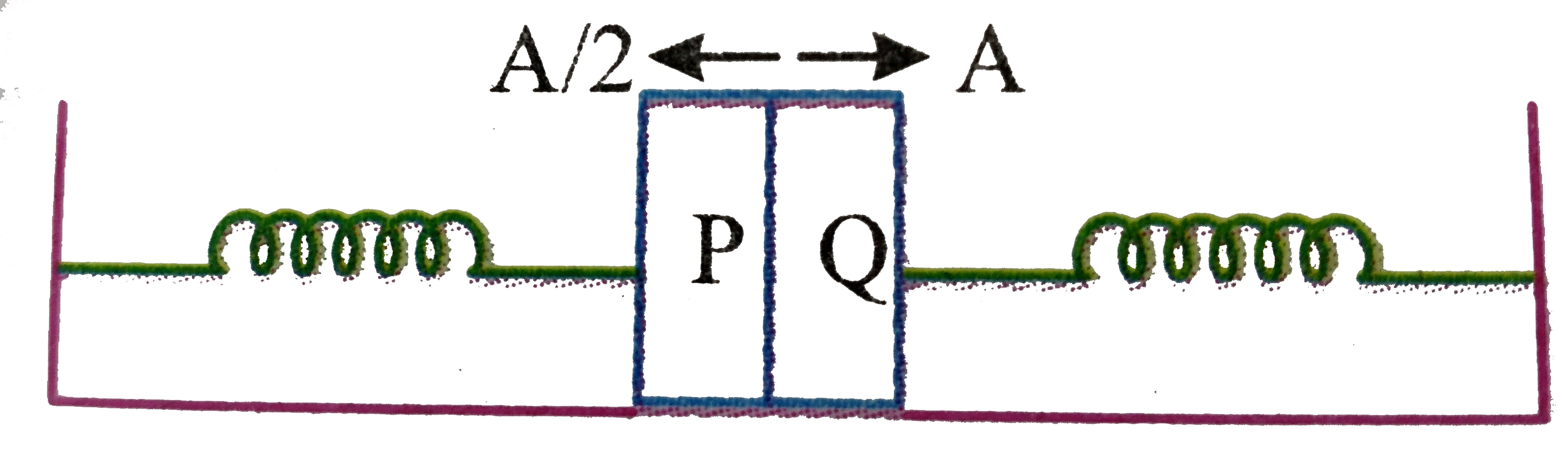
The time period of oscillation of combined mass is
View SolutionA shot putter with a mass of 80kg pushes the iron ball of mass of 6kg from a standing position accelerating it uniformly form rest at an angle of 45∘ with the horizontal during a time interval of 0.1 seconds. The ball leaves his hand when it 2m high above the level ground and hits the ground 2 seconds later (g=10m/s2).
The accleration of the ball in shot putter's hand .
View SolutionWhat is the discovery of CV Raman?
View SolutionTwo identical balls A and B eavh of mass 0.1 kg are attached to two identical mass less is springs. The spring-mass system is consetrained to move inside a right smooth pipe bent in the form of a circle as shown in figure . The pipe is fixed in a horigental plane. The center of the balls can move in a circle of radius 0.06 m . Each spring has a natural length of 0.06 pi m and force constant 0.1 N//m . Initially, both the balls are displaced bu an angle theta = pi//6 dadius withrespect to diameter PQ of the circle and released from rest. a. Calculate the frequency of oscillation of the ball B. b. What is the total energy of the system ? c. Find the speed of the bal A when A and B are at the two ends of the diameter PQ.
View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k , with the spring at its natural length. A third identical block C (mass m ) moving with a speed v along the line joining A and B collides with A . The maximum compression in the spring is
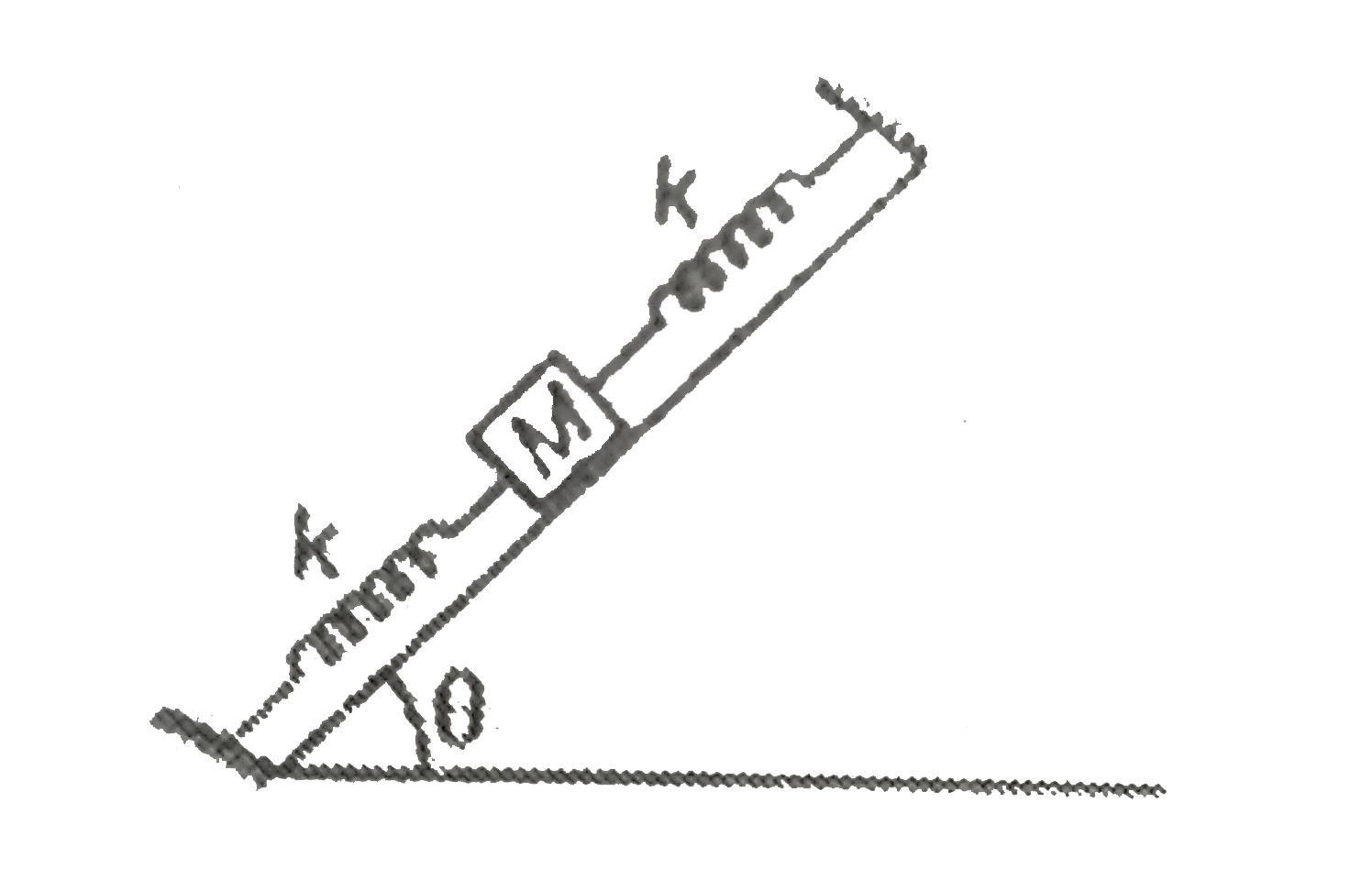
View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the spring are fixed to ffirm supports. If each spring has a force constant k, the period of oscillation of the body is: (assuming the spring as massless)
View SolutionA small ball of mass M=1 kg is attached to two identical springs of constant 100N//m , which are attached to floor and roof. The springs are initially unstretched. By what distance ball comes down to attain equilibrium? (in cm)
View SolutionOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is
View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
View SolutionOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K, the period of oscillation of the body (assuming the springs as massless) is :
View SolutionOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is

View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
View SolutionTwo identical balls A and B eavh of mass 0.1 kg are attached to two identical mass less is springs. The spring-mass system is consetrained to move inside a right smooth pipe bent in the form of a circle as shown in figure . The pipe is fixed in a horigental plane. The center of the balls can move in a circle of radius 0.06 m . Each spring has a natural length of 0.06 pi m and force constant 0.1 N//m . Initially, both the balls are displaced bu an angle theta = pi//6 dadius withrespect to diameter PQ of the circle and released from rest. a. Calculate the frequency of oscillation of the ball B. b. What is the total energy of the system ? c. Find the speed of the bal A when A and B are at the two ends of the diameter PQ.
View Solution
