A solid metallic sphere of radius R having charge +3Q is surrounded by a hollow spherical shell of radius 2R and having a charge −Q.
(a) Find electric field at distance r from centre of solid sphere [R<r<2R].
(b) Find potential difference between sphere and shell.
(c ) Find distribution of charge if
(i) inner sphere is earthed
(ii) inner sphere and shell are connected by a metallic wire.

To find electeric field at P, assume charge inside sphere of radius r to be concentrated at centre O.
EP=14π∈0.3Qr2
(b) VA=14π∈0[3QR+−Q2R]
VB=14π∈0[3Q2R+−Q2R]
VA−VB=14π∈0.3Q2R
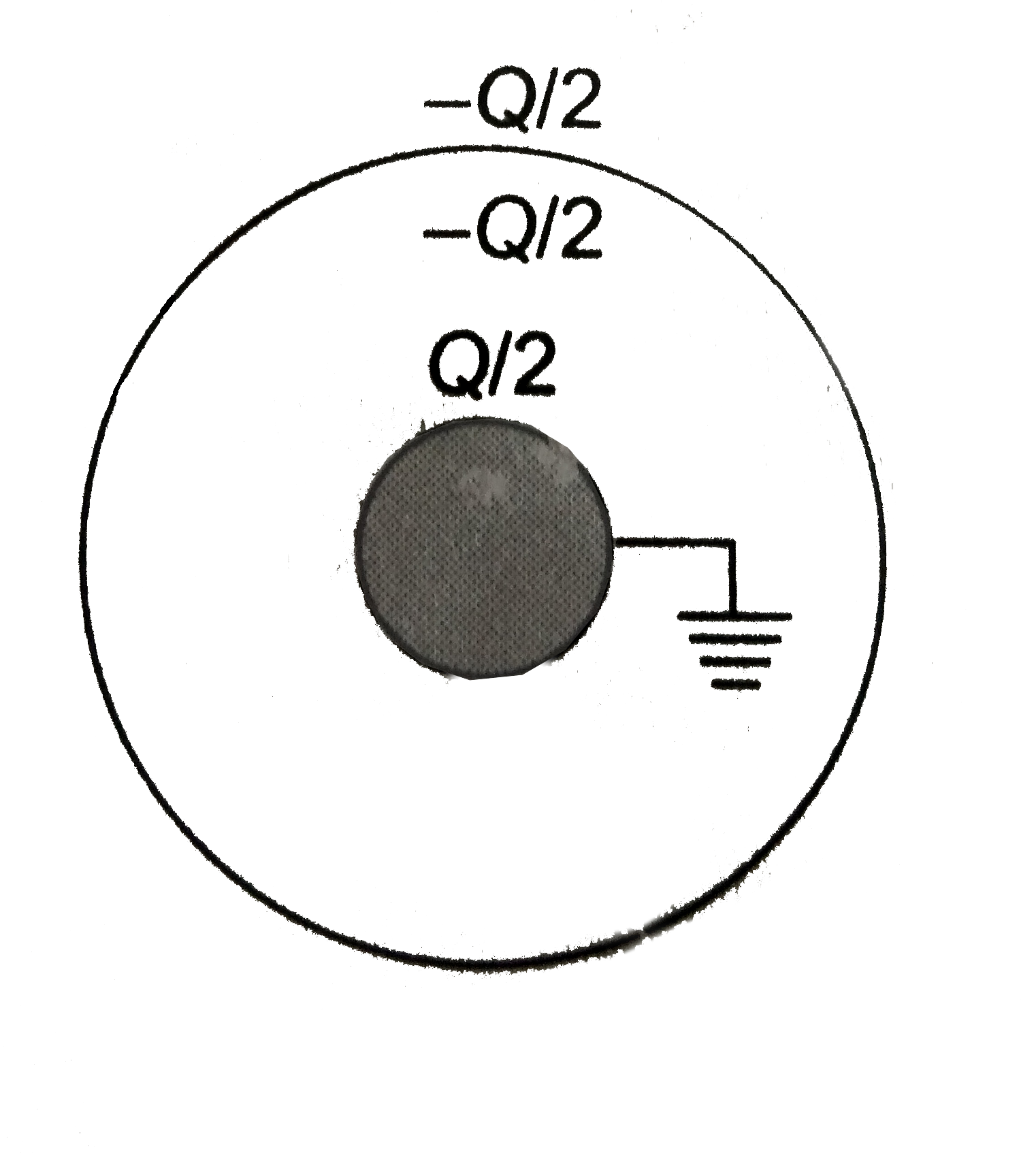
(c ) (i) Let charge on inner sphere be Q'.
VP=14π∈0[Q'R+−Q2R]=0
Q'=Q/2

Charge distribution :
(ii) When shell is connected to sphere , potential difference between shell and sphere becomes zero.

VA>VB , charge 3Q from sphere flows to shell , so that VA=VB
Charge on sphere =0
Charge on shell =2q
Similar Questions
A solid sphere of radius R has a charge +2Q. A hollow spherical concentric with the first sphere that has net charge -Q.
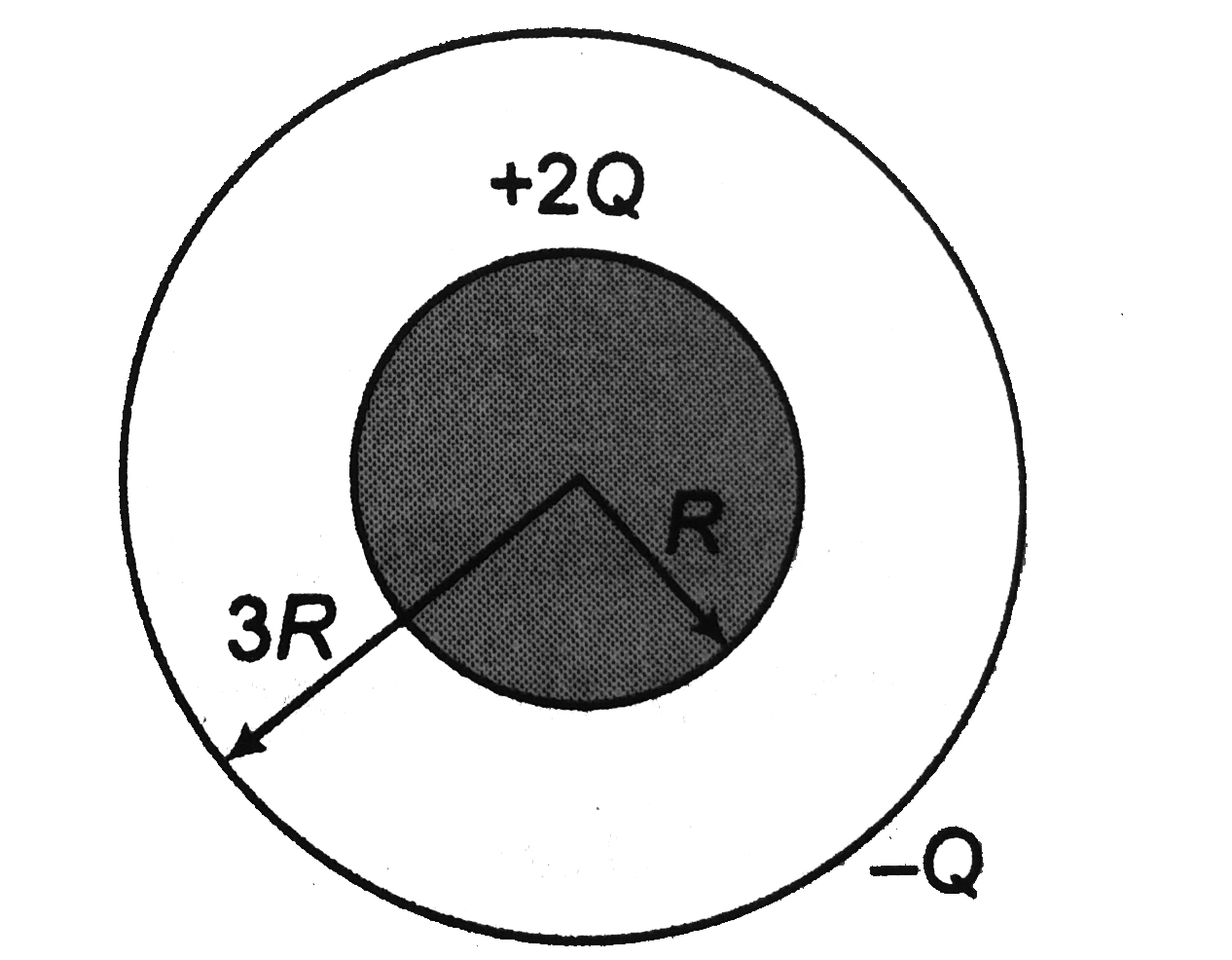
(a) Find the electric field between the spheres at a distance r from the centre of the inner sphere. [R<r<3R]
(b) Calculate the potential difference between the spheres.
(c) What would be the final distribution of charges, if a conducting wire joins the spheres?
(d) Instead of (c), if the inner sphere is earthed, what is the charge on it?
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View Solution
Knowledge Check
A metallic sphere of radius R having charge Q is connected to an uncharged sphere of radius 3R. The amount of charge flown through connecting wire is
AQ/4BQ/2C3Q/4DQA spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge Q(R>r0. The potential difference between the two is
AProportional to QBProportional to qCDependent on both Q and qDIndependent of both Q and qA spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge Q (R > r). The potential difference between the two is
Aproportional to QBProportional to qCDependent on both Q and qDindependent of both Q and q
If the potential at the center of a uniformly charged sphere of radius R is V then electric field at a distance r from the center of sphere will be (r<R) : -
View SolutionMetallic sphere of radius R is charged to potential V. Then charge q is proportional to
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View Solution

