A horizontal wire AB which is free to move in a vertical plane and carries a steady current of i2A, is in equilibrium at a height of h over another parallel long wire CD, which is fixed in a horizontal plane and carries a steady current of i1A as shown. Show that when AB is slightly depressed and released it executes simple harmonic motion. Find the period of oscillations.


Since upper wire is in equilibrium, for this currents in wires should be un opposite directions.
Magnetic force per unit length between wires
μ0i1i22πh, upwards
Let mass of unit length of wire =λ
Weight of upper wire per unit length =λg downward
In equilibrium, μ0i1i22πh=λg ...(i)
Let AB be slightly depressed by x
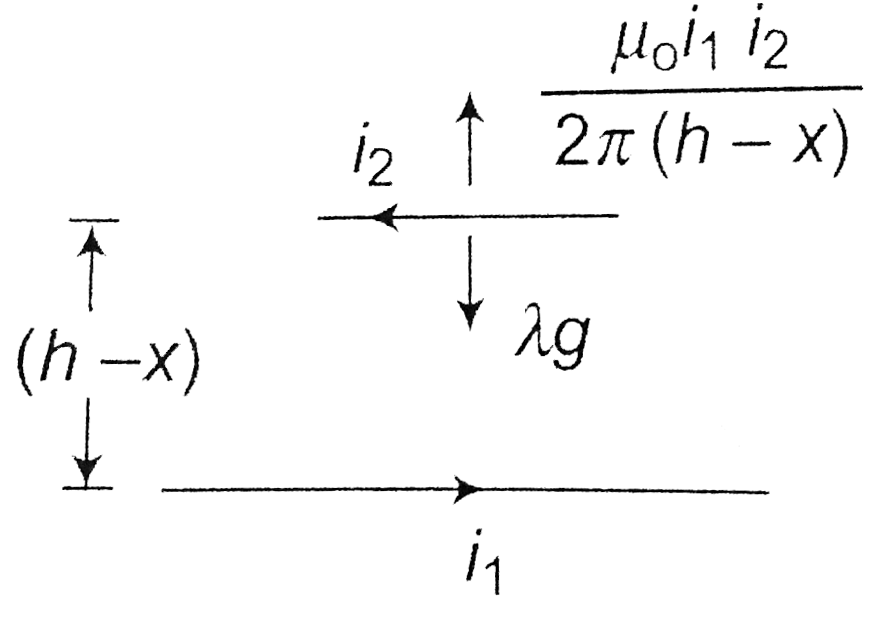
Restoring force F=−[μ0i1i22π(h−x)−λg]
=−[μ0i1i22πh(1−x/h)−λg]
=−[μ0i1i22πh(1−xh)−λg]
=−[λg(1−xh)−1−λg]
=−λg[(1−xh)−1−1]
=−λg[1−xh−1]=λghx (since x<<h)
a=Fλ=−ghx
aα−x (case of S.H.M), (a=−ω2x)
T=2π√hg
Topper's Solved these Questions
Similar Questions
A positively charged particle projected towards east is deflected towards north by a magnetic field. The field may be
View SolutionThe magnetic field at the origin due to a current element I→dl placed at position r is
(i) (μ0i4π)(d→l×→rr3)
−(μ0i4π)(d→l×→rr3)
(iii) (μ0i4π)(→r×d→lr3)
−(μ0i4π)(→r×d→lr3)
View SolutionThe electric field in a certain region is acting radially outwards and is given by E=Ar.A charge contained in a sphere of radius 'a' centred at the origin of the field, will given by
View SolutionA long current carrying wire , carrying current I_(1) such that I_(1) is flowing out from the plane of paper is placed at O . A steady state current I_(2) is flowing in the loop ABCD
View SolutionA long horizontal wire AB , which is free to move in a vertical plane and carries a steady current of 20 A , is in equilibrium at a height of 0.01 m over another parallel long wire CD which is fixed in a horizontal plane and carries a steady current of 30 A , as shown in figure. Shown that when AB is slightly depressed, it executes simple harmonic motion. Find the period of oscillations.
View SolutionA long horizontal wire AB,which is free to move in a vertical plane and carries a steady current of 20A, is in equilibrium at a height of 0.01m over another paralllel long wire CD which is fixed in a horizontal plane and carries a steady current of 30A, as shown in figure. Show that when AB is slightly
depressed it executes simple harmonic motion. Find the period of oscillations.

View SolutionA long straight wire carries a steady current I_(1) Nearby is a rectangular loop that carries a steady current I2 The directions of the two currents are shown in the figure.
 Which statement is /are false?
Which statement is /are false?
View SolutionTwo long wire AB abd CD carry currents i_(1) and i_(2) in the direactions show in figure
View SolutionA long horizontal wire AB which is free to move in a vertical plane and carries a steady current of 20 A ,is in equilibrium at a height of 0.01 m over another parallel infinitely long wire CD ,which is fixed in a horizontal plane and carries a steady current of 30 A .Show that when AB is slightly depressed, it executes simple harmonic motion.the period of oscillations is 1/N seconds.then find the value of N .(Use pi^(2)=10 & g=10 m//s^(2) )
View SolutionA rectangular loop carrying a current i_(2) situated near a long straight wire carrying a steady current i_(1) . The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
View SolutionA horizontal wire AB of length T and mass 'm' carries a steady current I_1 free to move in vertical plane is in equilibrium at a height of 'h' over another parallel long wire CD carrying a steady current I_2 which is fixed in a horizontal plane as shown. Derive the expression for the force acting per unit length on the wire AB and write the condition for which wire AB is in equilibrium.
View SolutionLet I1andI2 be the steady currents passing through a long horizontal wire XY and PQ respectively. The wire PQ is fixed in horizontal plane and the wire XY be is allowed to move freely in a vertical plane. Let the wire XY is in equilibrium at a height d over the parallel wire PQ as shown in figure.
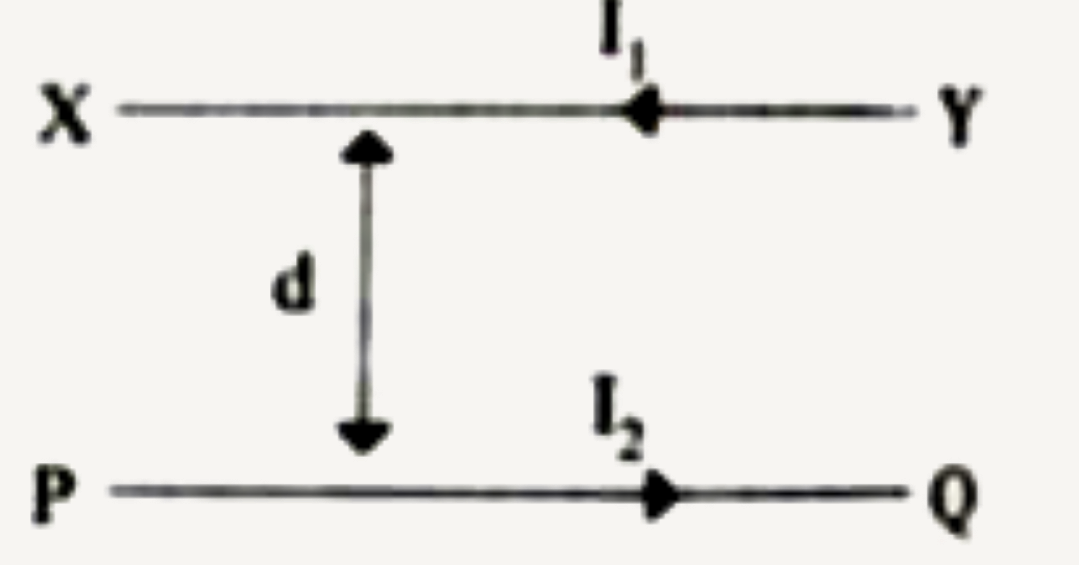
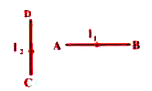
View SolutionA current I1 carrying wire AB is placed near another long wire CD carrying current I2. If wire AB is free to move, it will have
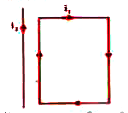
View SolutionA rectangular loop carrying a current i1, is situated near a long striaght wire carrying a steady current i2. The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
View SolutionA long horizontal wire AB ,which is free to move in a vertical plane and carries a steady current of 20 A , is in equilibrium at a height of 0.01 m over another paralllel long wire CD which is fixed in a horizontal plane and carries a steady current of 30 A , as shown in figure. Show that when AB is slightly depressed it executes simple harmonic motion. Find the period of oscillations.
View Solution

