The parabolic path of a projectile is represented by y=x√3−x260 in MKS units: Its angle of projection is (g=10ms−2)
30∘
45∘
60∘
90∘
The correct Answer is:A
To find the angle of projection from the given parabolic path of the projectile, we can follow these steps:
Step 1: Understand the given equation
The equation of the projectile's path is given as:
y=x√3−x260
Step 2: Compare with the standard trajectory equation
The standard form of the trajectory of a projectile is:
y=xtanθ−gx22v2cos2θ
where g is the acceleration due to gravity, v is the initial velocity, and θ is the angle of projection.
Step 3: Identify the coefficients
From the given equation, we can identify:
- The coefficient of x is 1√3, which corresponds to tanθ.
- The coefficient of x2 is −160, which corresponds to −g2v2cos2θ.
Step 4: Find tanθ
From the comparison, we have:
tanθ=1√3
Step 5: Calculate the angle θ
To find θ, we take the arctangent:
θ=tan−1(1√3)
Step 6: Determine the angle in degrees
From trigonometric values, we know:
tan30∘=1√3
Thus,
θ=30∘
Final Answer
The angle of projection is 30∘.
---
The equation of the projectile's path is given as:
y=x√3−x260
The standard form of the trajectory of a projectile is:
y=xtanθ−gx22v2cos2θ
where g is the acceleration due to gravity, v is the initial velocity, and θ is the angle of projection.
From the given equation, we can identify:
- The coefficient of x is 1√3, which corresponds to tanθ.
- The coefficient of x2 is −160, which corresponds to −g2v2cos2θ.
From the comparison, we have:
tanθ=1√3
To find θ, we take the arctangent:
θ=tan−1(1√3)
From trigonometric values, we know:
tan30∘=1√3
Thus,
θ=30∘
The angle of projection is 30∘.
Similar Questions
Knowledge Check
The trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Angle of projection θ is :-A30∘B60∘C45∘D√3 radThe equation of a projectile is y=√3x−gx22
the angle of projection is:-A30∘B60∘C45∘DnoneThe horizontal range of a projectile is 4√3 times its maximum height. Its angle of projection will be
A45∘B60∘C90∘D30∘
The horizontal range of a projectile is 4√3 times its maximum height. The angle of projection is
View SolutionThe equation of trajectory of an oblique projectile y=√3x−gx22. The angle of projection is
View SolutionEquation of trajector of ground to ground projectile is y=2x−9x2. Then the angle of projection with horizontal and speed of projection is : (g=10m/s2)
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Time of flight of the projectile is :-
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]
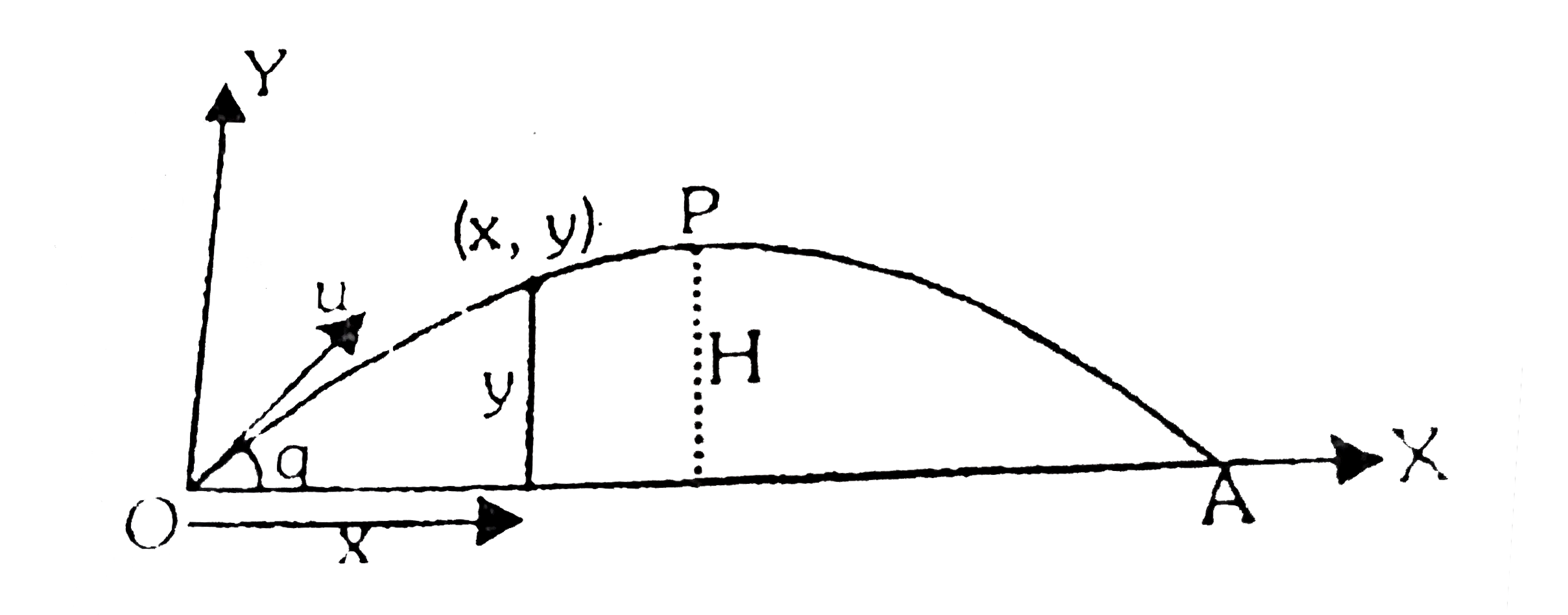
Range OA is :-
View Solution

