let B be the magnetic field at a point between the two conductors, at a distance x from the axis. Let B2 be the magnetic field at a point outside conductor, at a distance 2x from the axis
B1=B2
B1=2B2
B2=2B1
B2=4B1
The correct Answer is:A
B1=μ0I2πx,B2=μ0(2I)2π(2x)=μ0I2πx
B1=B2
Similar Questions
(a) How does the magnetic field (B) due to a straight conductor vary with distance (r) from it?
(b) How does the magnetic field (B) vary inside a solenoid?
View SolutionA cylindrical conductor of radius 'R' carries a current 'i'. The value of magnetic field at a point which is R/4 distance inside from the surface is 10T. Find the value of magnetic field at point which is 4R distance outside from the surface
View Solution
Knowledge Check
Magnetic field at a point on the line of current carrying conductor is
AmaximumBinfinityCzeroDfinite valueThe magnetic field due to a short magnet at a point in its axis at distance X cm from the middle of the magnet is
A100 GaussB400 GaussC50 GaussD200 GaussA current i ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor of the cable, then the magnetic induction at any point outside the conductor at a distance r meter from the axis is
A∞BZeroCμ04π2irDμ04π2πrr
The same current I flows in two long parallel conductors at a distance 2d, as shown. The strength of the magnetic field at a point P, equidistant from both conductors, is
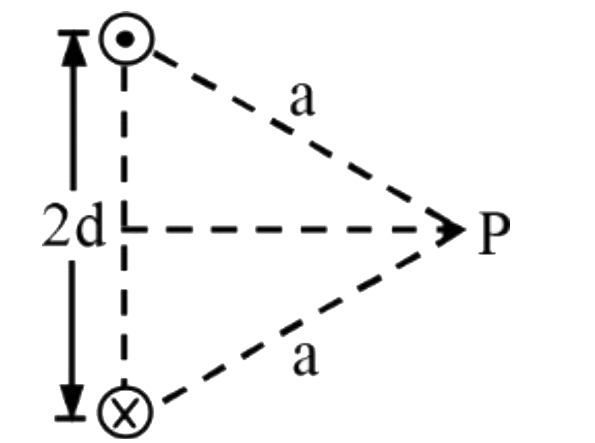
View SolutionA current flows in a conductor from east to west. The direction of the magnetic field at a points above the conductor is
View SolutionMagnetic field at the centre of a circular coil of radius R due to curent i flowing through it is B. The magnetic field at a point along the axis at distance R from the centre is :
View SolutionThe magnetic field on the axis of a circular current carrying conductor of radius r at a distance r from centre is Ba and the magnetic field at its centre is Bc. The value of Ba:Bc is
View SolutionPoints A and B are located along a line perpendicular to the axis of a small bar magnet. Line joining the points A and B is passing through the centre of bar magnet. Point A is at a distance x from the centre of magnet on one side and point B is on the other side of magnet at a distance 3x from the centre of magnet. If B1 and B2 are the magnetic field intensities at A and B respectively then find approximate value of B1:B2
View Solution

