A rod CD of length b carrying a current I2 is placed in a magentic field due to a thin long wire AB carrying current I1 as shown in figure. Then find the net force experience by the wire
Video Solution
Text Solution
 Magnetic induction due to a straight wire at a positiion of small element dx at a distance x from the conductor AB is μ02πI1x . Force on the current element is −→dF=dBI2dxsin90∘,
Magnetic induction due to a straight wire at a positiion of small element dx at a distance x from the conductor AB is μ02πI1x . Force on the current element is −→dF=dBI2dxsin90∘,
μ02πI1I2xdx. Net force on conductor is F=a+b∫aμ02πI1I2xdx
=μ02πI1I2[logx]aa+b=μ02πI1I2log(1+ba)
|
Similar Questions
Knowledge Check
The magnetic field intensity due to a thin wire carrying current I shown in figure, is
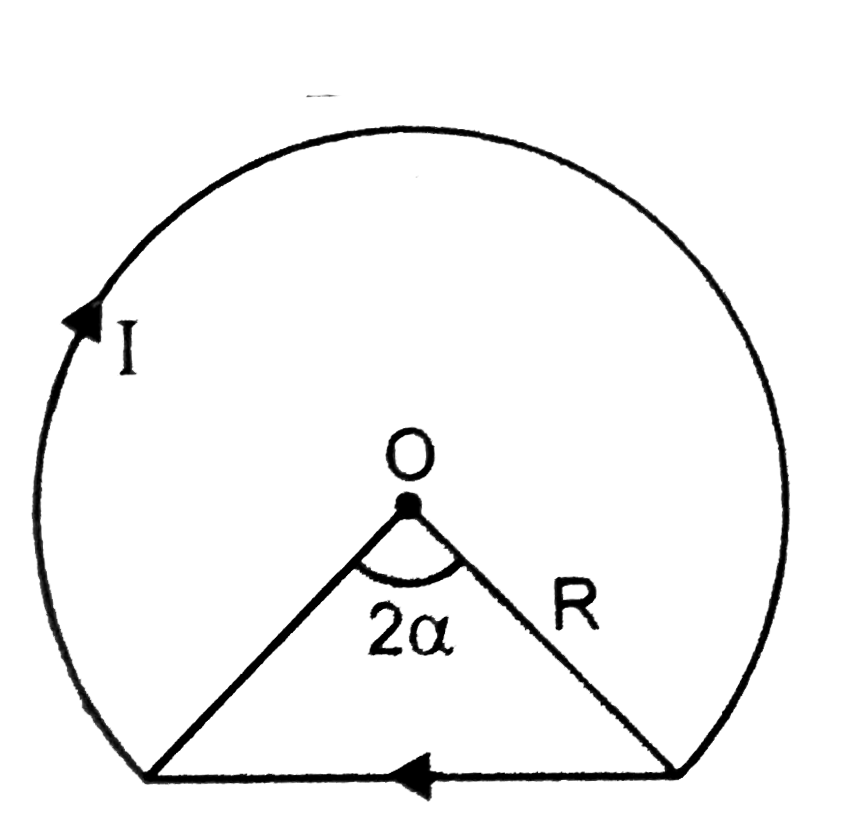 Aμ0I2πR[π−α+tanα]Bμ0I2πR[π−α]Cμ0I2πR[π+α]Dμ0I2πR[π+α−tanα]
Aμ0I2πR[π−α+tanα]Bμ0I2πR[π−α]Cμ0I2πR[π+α]Dμ0I2πR[π+α−tanα]A segment AB of wire carrying current I1 is placed perpendicular to a long straight wire carrying current I2 as shown in figure. The magnitude of force experienced by the straight wire AB is
 Aμ0I1I22πln3Bμ0I1I22πln2C2μ0I1I22πDμ0I1I22π
Aμ0I1I22πln3Bμ0I1I22πln2C2μ0I1I22πDμ0I1I22πA field due to a long straight wire carrying a current I is proportional to
AlBl2Cl3D√l
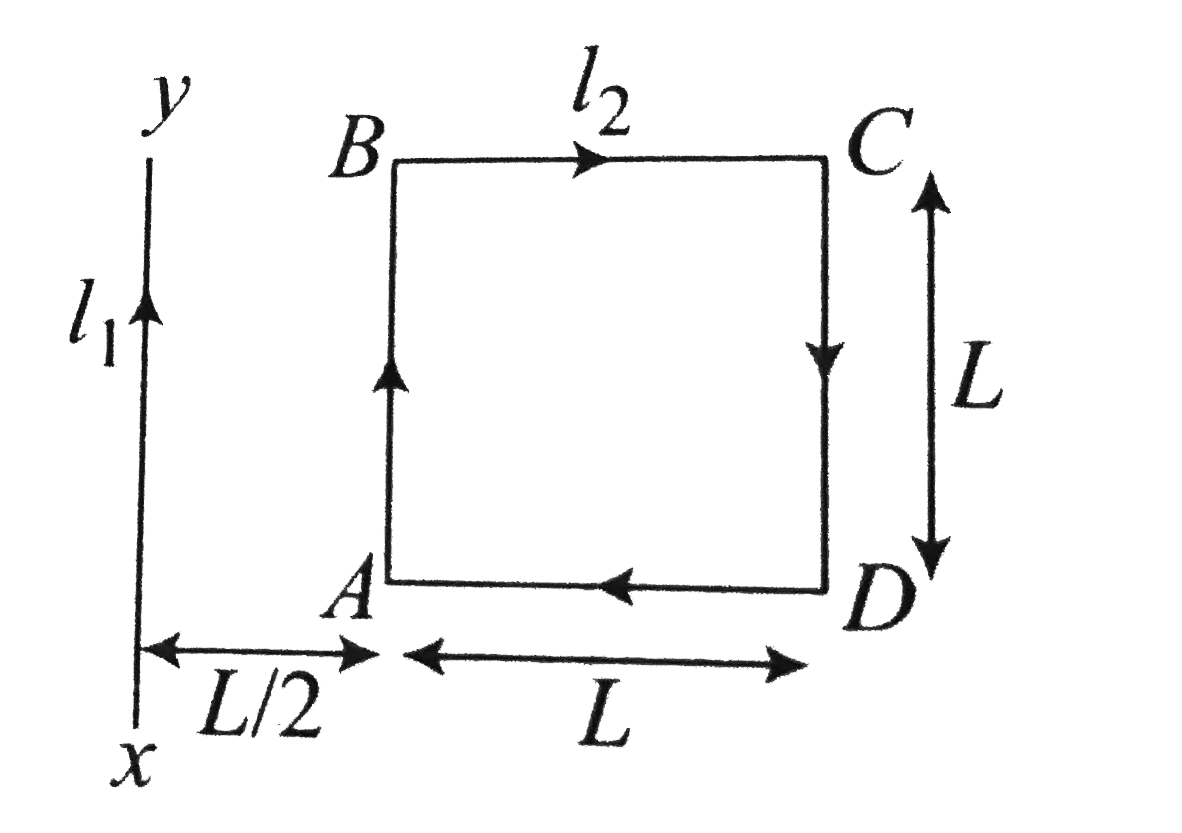
A square loop ABCD, carrying a current I2 is placed near and coplanar with a long straight conductor XY, carrying a current I1 as shown in Figure. The net force on the loop will be
View SolutionThe field due to a long straight wire carrying a current I is proportional to
View SolutionThe field due to a long straight wire carrying a current I is proportional to
View SolutionA conductor AB of length L carrying a current I', is placed perpendicular to a long straight conductor XY carrying a current I as shown in Fig. The forces on AB has magnitude

View SolutionThe direction of magnetic field at a point due to an infinitely long wire carrying current is
View Solution



