A particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(π3B0α) would be
√32υ0B0α+√32υ0(t−πB0α)
√32υ0B0α+υ0(t−π3B0α)
√32υ0B0α+υ02(t−π3B0α)
√32υ0B0α+υ0t2
The correct Answer is:C
r=mυ0B0q=υ0B0α
xr=√32=sinθ
∴θ=60∘ tOA=T6=π3B0α

Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - LEVEL-VI (SINGLE ANSWER QUESTION)
81 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Level =I (H.W)
42 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT Based Questions
20 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
A battery is connected between two points AandB on the circumference of a uniform conducting ring of radius r and resistance R . One of the arcs AB of the ring subtends an angle θ at the centre . The value of the magnetic induction at the centre due to the current in the ring is
View SolutionA north pole of strengtπAm, is moved around a circle of radius 10cm which lies around a long straight conductor carrying a current of 10A. The work doen is nearly
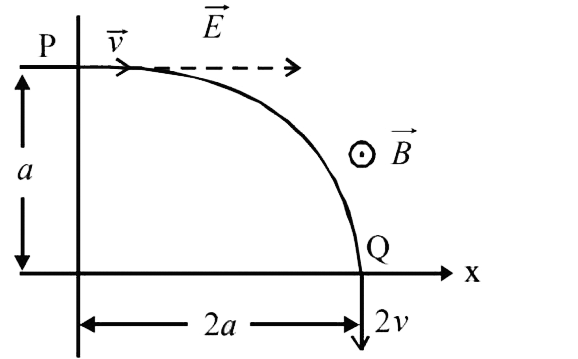
View SolutionA particle of charge +q and mass m moving under the influence of a uniform electric field Eˆi and uniform magnetic field Bˆk follows a trajectory from P→Q as shown in fig. The velocities at PandQ are vˆi and −2vˆj . which of the following statement(s) is/are correct ?
View SolutionA paramagnetic sample shows a net magnetisation of 8Am−1 when placed in an external magnetic field of 0⋅6T at a temperature of 4K. When the same sample is placed in an external magnetic field of 0⋅2T at a temperature of 16K, the magnetisation will be
View SolutionA nucleus splits into two nuclear parts having radii in the ratio 1:2 Their velocities are in the ratio
View SolutionSuppose a nucleus initally at rest undergoes α decay according to equation
.23592X→Y+α
At t=0, the emitted α-partilces enter a region of space where a uniform magnetic field →B=B0ˆj and elcertis field →E=E0ˆi exist. The α-prticles enters in the region with velocity →V=v0ˆj from x=0. At timet=√3×106m0q0E0s, the particle was observed to have speed twice the initial velocity v0. Then, find (a) the velocity v0 of the α-particles,
(b) the initial velocity v0 of the α-particle, (c ) the binding energy per nucleon of the α-particle.
[Given thatm(Y)=221.03u,m(α)=4.003u,m(n)=1.09u,m(P)=1.008u].
View SolutionA particle of charge per unit mass alpha is released from origin with a velocity vecv=v_(0)hati uniform magnetic field vecB=-B_(0)hatk . If the particle passes through (0,y,0) , then y is equal to
View SolutionA particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(π3B0α) would be
View SolutionThe position of a particle at time t, is given by the equation, x(t) = (v_(0))/(alpha)(1-e^(-alpha t)) , where v_(0) is a constant and alpha gt 0 . The dimensions of v_(0) & alpha are respectively.
View SolutionA charged particle of specific charge (Charge/mass) alpha is released from origin at time t=0 with a velocity given as vecv=v_(0)(hati+hatj) The magnetic field in region is uniform with magnetic induction vecB=B_(0)hati . Coordinates of the particle at time t=(pi)/(B_(0)alpha) are:
View SolutionA particle of specific charge 'α' is projected from origin at t=0 with a velocity →V=V0(ˆi−ˆk) in a magnetic field →B=−B0ˆk. Then : (Mass of particle =1 unit)
View SolutionA charge praticule of sepeific charge (charge/ mass ) alpha is realsed from origin at time t=0 with velocity v= v_(0)(hati+hatj) in unifrom magnetic fields B= B_(0)hati . Co-ordinaties of the particle at time t = (pi)/(B_(0)alpha) are
View SolutionA charged particle (q.m) released from origin with velocity v=v_(0)hati in a uniform magnetic field B=(B_(0))/(2)hati+(sqrt3B_(0))/(2)hatJ . Pitch of the helical path described by the particle is
View SolutionA charged particle (q.m) released from origin with velocity v=v_(0)hati in a uniform magnetic field B=(B_(0))/(2)hati+(sqrt3B_(0))/(2)hatJ . Maximum z-coordinate of the particle is
View SolutionA particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(π3B0α) would be
View SolutionChoose the correct option: A particle of charge per unit mass alpha is released from origin with a velocity vecv=v_(0)hati in a magnetic field vec(B)=-B_(0)hatk for xle(sqrt(3))/2 (v_(0))/(B_(0)alpha) and vec(B)=0 for xgt(sqrt(3))/2 (v_(0))/(B_(0)alpha) The x -coordinate of the particle at time t((pi)/(3B_(0)alpha)) would be
View Solution

