A closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as →μ=−→IA where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field →B, then torque acting on the loop is given by →τ=→μ×→B. Now answer the following questions:
A uniformly charged insulating ring is rotated in a uniform magnetic field about its own axis, then
Ring will experience a magnetic force
Ring must be experience a magnetic torque
Ring may experience a magnetic torque
None of the above
The correct Answer is:C
τ=MBsinθ, Rotating ring will behave as a magnetic pole.
Similar Questions
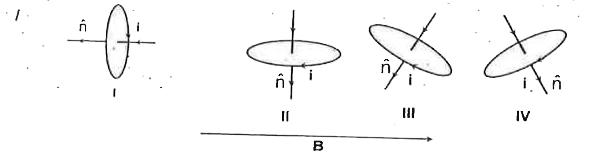
As shown in the figure four idential loops are placed in a uniform magnetic field →B. The loops carry equal current I. →n denotes the normal to the plane of each loop. Potential energies in descending order are
View SolutionA rectangle loop of size l×b carrying a steady current I is placed in a uniform magnetic field →B. Prove that the torque →τ acting on the loop is given by →τ=→m×→B, where →m is the magnetic moment of the loop.
View SolutionDerive the expression for the torque τ acting on a rectangular current loop of area A placed in a uniform magnetic field B. Show that →τ=→m×→B where →m is the moment of the current loop given by →m=→IA.
View SolutionAssertion : The net magnetic force on a current loop in a uniform magnetic field is zero but torque may or may not be zero.
Reason : Torque on a current carrying coil in a magnetic field is given by →τ=nI(→AX→B).
View SolutionA rectangular loop carrying a current i is placed in a uniform magnetic field B. The area enclosed by the loop is A. If there are n turns in the loop, the torque acting on the loop is given by
View SolutionA closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as →μ=−→IA where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field →B, then torque acting on the loop is given by →τ=→μ×→B. Now answer the following questions:
A uniformly charged insulating ring is rotated in a uniform magnetic field about its own axis, then
View SolutionA closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as vec(mu) = vec(IA) where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field vec(B) , then torque acting on the loop is given by vec(tau) = vec(mu) xx vec(B) . Now answer the following questions: Consider the situation shown in Fig., ring is having a uniformly distributed positive charge. Magnetic field is perpendicular to the axis of ring. Now ring is rotated in anticlockwise direction as seen from left hand side direction of magnetic torque acting on the ring is
View SolutionA closed current-carrying loop having a current I is having area A. Magnetic moment of this loop is defined as →μ=−→IA where direction of area vector is towards the observer if current is flowing in anticlockwise direction with respect to the observer. If this loop is placed in a uniform magnetic field →B, then torque acting on the loop is given by →τ=→μ×→B. Now answer the following questions:
Let ring in the above question is having a radius R and a charge Q is uniformly distributed over it. Ring is rotated with a constant angular velocity (ω) as mentioned above.
Torque acting on the ring due to magnetic force is
View Solution

