ABC is a triangle and EF is any straight line parallel to BC meeting AC, AB in E,F respectively. If BRandCQ be drawn parallel to AC, AB respectively to meet EF in R and Q respectively,prove that ΔARB=ΔACQ.
Step by step video & image solution for ABC is a triangle and EF is any straight line parallel to BC meeting AC, AB in E,F respectively. If BR and CQ be drawn parallel to AC, AB respectively to meet EF in R and Q respectively,prove that DeltaARB =DeltaACQ. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
XY is a line parallel to side BC of a triangle ABC. If BE||AC and CF ||AB meet XY at E and F respectively , show that ar(ABE)=ar(ACF)

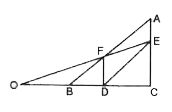
View Solutionयदि त्रिभुज ABC की भुजा BC पर कोई बिंदु D हैं। इस बिंदु से AC औरAB भुजाओं के समान्तर रेखाएं DF और DE खींची जाएं जो त्रिभुज की भुजा और AB को क्रमशः E तथा F पर काटती हैं। यदि EF और BC को आगे बढ़ाया जाए तो ये बिंदु O पर मिलती हैं। सिद्ध कीजिए कि OD2=OB.OC
View SolutionΔABC में, AD एक माध्यिका है । ∠ADB और ∠ADC के समद्विभाजक क्रमशः AB एवं AC से E एवं F बिन्दु पर मिलते है । सिद्ध कीजिए कि EF∣∣BC है ।
View SolutionDelta ABC In, E and F are the midpoints of AC and AB respectively. The heading AP AP inserted on BC intersects EF on Q. Prove that AQ = QP
View Solutionएक त्रिभुज ABC में, AD एक मध्यिका है। ∠ADB और ∠ADC के कोण अर्द्धक AB और AC को क्रमश: E व F पर मिलते है। AE:BE=3:4,EF:BC=?
View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Find AB, if EF=4.8cm.
View SolutionThe side AC of a triangle ABC is produced to point E so that CE=12 AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that:
3DF=EF
View SolutionThe side AC of a triangle ABC is produced to point E so that CE=12 AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that:
4CR=AB
View Solution
