In Fig. 4.145 (a) ABC is right angled at C and DE⊥AB . Prove that ABCADE and hence find the lengths of AE and DE . (FIGURE)
To solve the problem, we need to prove that triangles ABC and ADE are similar and then find the lengths of AE and DE.
Step 1: Prove that triangles ABC and ADE are similar.
1. Identify the angles:
- Triangle ABC is a right triangle with the right angle at C, so ∠ACB = 90°.
- DE is perpendicular to AB, so ∠AED = 90°.
- Therefore, ∠ACB = ∠AED = 90°.
2. Common angle:
- Angle A is common to both triangles ABC and ADE, so ∠A = ∠A.
3. Angle-Angle (AA) Criterion:
- Since we have two angles in triangle ABC that are equal to two angles in triangle ADE, we can conclude by the AA criterion that triangle ABC is similar to triangle ADE.
- Thus, we write:
△ABC∼△ADE
Step 2: Use the properties of similar triangles to find AE and DE.
1. Set up the proportion:
- From the similarity of the triangles, we know that the ratios of corresponding sides are equal:
ABAD=ACAE=BCDE
2. Assign known lengths:
- Let’s assume the lengths:
- AB = c (hypotenuse)
- AC = 5 (one leg)
- BC = 12 (other leg)
- AD = 3 (one leg of triangle ADE)
3. Calculate AB using Pythagorean theorem:
- Since triangle ABC is a right triangle, we can use the Pythagorean theorem:
AB2=AC2+BC2
AB2=52+122=25+144=169
AB=√169=13
4. Set up the equations:
- Using the similarity ratios:
ABAD=ACAE
Substituting the known values:
133=5AE
Cross-multiplying gives:
13⋅AE=3⋅5
13⋅AE=15
AE=1513
5. Find DE using the second ratio:
BCDE=ABAD
Substituting the known values:
12DE=133
Cross-multiplying gives:
12⋅3=13⋅DE
36=13⋅DE
DE=3613
Final Results:
- Length of AE = 1513 cm
- Length of DE = 3613 cm
- Triangle ABC is a right triangle with the right angle at C, so ∠ACB = 90°.
- DE is perpendicular to AB, so ∠AED = 90°.
- Therefore, ∠ACB = ∠AED = 90°.
- Angle A is common to both triangles ABC and ADE, so ∠A = ∠A.
- Since we have two angles in triangle ABC that are equal to two angles in triangle ADE, we can conclude by the AA criterion that triangle ABC is similar to triangle ADE.
- Thus, we write:
△ABC∼△ADE
- From the similarity of the triangles, we know that the ratios of corresponding sides are equal:
ABAD=ACAE=BCDE
- Let’s assume the lengths:
- AB = c (hypotenuse)
- AC = 5 (one leg)
- BC = 12 (other leg)
- AD = 3 (one leg of triangle ADE)
- Since triangle ABC is a right triangle, we can use the Pythagorean theorem:
AB2=AC2+BC2
AB2=52+122=25+144=169
AB=√169=13
- Using the similarity ratios:
ABAD=ACAE
Substituting the known values:
133=5AE
Cross-multiplying gives:
13⋅AE=3⋅5
13⋅AE=15
AE=1513
BCDE=ABAD
Substituting the known values:
12DE=133
Cross-multiplying gives:
12⋅3=13⋅DE
36=13⋅DE
DE=3613
- Length of AE = 1513 cm
- Length of DE = 3613 cm
Similar Questions
In Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD

View SolutionIn Figure, AD is the median and DE∣∣AB . Prove that BE is the median.
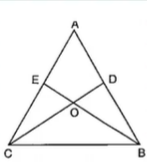
View SolutionIn Figure, it is given that AE=AD and BD=CE. Prove that AEB≅ADC
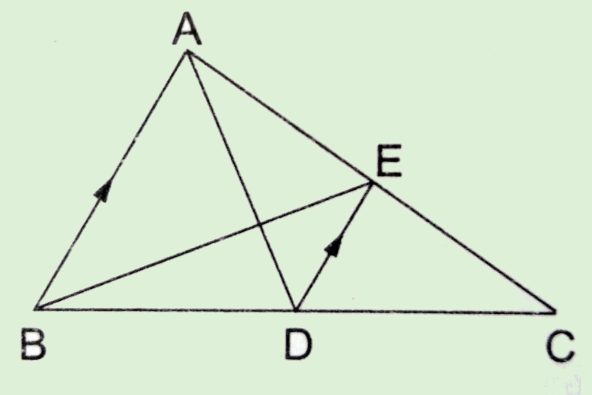
View SolutionIn Figure, AD and BE are medians of ABC and BE∣∣DF . Prove that CF=14AC
Consider △ABC Since AD is Median
⇒BD=BC⋯(1)
Since BE is Median⇒AE=EC⋯(2)
Consider △BECSince BE∣∣DF
By Basic Proportionality theorm, ⇒BDDC=EFFC
From (1)⇒CF=EF
⇒CF=12AE
From (2)⇒CF=14AC
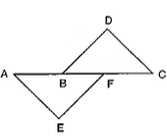
View SolutionIn Figure, it is given that AB=CF, EF=BD and ∠AFE= ∠CBD. Prove that AFE= ≅CBD
View SolutionIn Figure, it is given that AB=BC and AD=EC. Prove that abe ≅CBD (ii) BD=BE

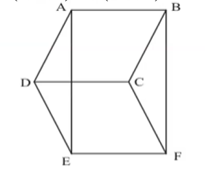
View SolutionIn Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
View SolutionIn Figure, it is given that AB=EF,BC=DE,AB⊥BD and FE⊥CE. Prove that ABD≅FEC.
View SolutionABCD is a rhombus, EABF is a straight line such that EA=AB=BF . Prove that ED and FC when produced meet at right angles.
View SolutionIn Figure, triangle ABC is right-angled at B. Give that AB=9CM, AC=15CM,andD,E are the mid-points of the sides ABandAC respectively, calculate
The length of BC
(ii) The area of ADE
View Solution