In Fig. 4.237, LM=LN=46o . Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively. (FIGURE)
To express x in terms of a, b, and c where a, b, and c are the lengths of LM, MN, and NK respectively, we can follow these steps:
1. Identify the Triangles: We have two triangles to consider: triangle KPN and triangle KLM.
2. Identify Common Angles: Notice that angle ∠NKP is equal to angle ∠KLM because they are both angles at point K (common angle).
3. Identify Given Angles: We know that ∠KLM=∠NKP=46∘.
4. Establish Similarity: Since two angles of triangle KPN are equal to two angles of triangle KLM, we can conclude that triangle KPN is similar to triangle KLM by the Angle-Angle (AA) similarity criterion.
5. Set Up Proportions: From the similarity of triangles, we can set up the following proportion based on the corresponding sides:
KNKM=PNLM
6. Substitute Known Lengths: We know that:
- KN=c
- KM=MN+NK=b+c
- PN=x
- LM=a
Substituting these into the proportion gives:
cb+c=xa
7. Cross Multiply: To solve for x, we cross multiply:
c⋅a=x⋅(b+c)
8. Isolate x: Rearranging the equation to solve for x:
x=acb+c
Final Expression:
Thus, we have expressed x in terms of a, b, and c:
x=acb+c
KNKM=PNLM
- KN=c
- KM=MN+NK=b+c
- PN=x
- LM=a
cb+c=xa
c⋅a=x⋅(b+c)
x=acb+c
Thus, we have expressed x in terms of a, b, and c:
x=acb+c
Similar Questions
In Fig. 4.237, LM=LN=46o . Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively. (FIGURE)
View SolutionIn Fig. 10.60, PA and PB are tangents from an external point P to a circle with centre O . LN touches the circle at M . Prove that PL+LM=PN+MN . (FIGURE)
View Solution
Knowledge Check
In the figure , l||m & l||n then x is -
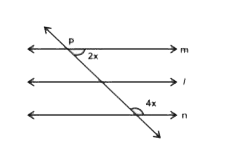 A90∘B45∘C30∘D60∘
A90∘B45∘C30∘D60∘Area of a rectangle =L×B
Perimeter of a rectangle = 2(L + B) where L and B are the length and breadth of the rectangle respectively.
The breadth of a rectangle of length 4 m and area 8.4m2 isA2.1 mB1.2mC4.2m2D2.1m2
In Fig. 60, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively. If ∠LMD=350 find ∠PLA.
View SolutionIn a ABC , If LandM are points on ABandAC respectively such that LMparallel BC
Prove that: ar(LOB)=ar(MOC)
View SolutionIn a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LCM)=ar(LBM)
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM . Prove that LM and BD bisect each other.
View SolutionIn a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LBC)=ar(MBC)
View SolutionABC is a right-angled triangle in which ∠B=900 and BC=a. If n points L1,L2,,LnonAB is divided in n+1 equal parts and L1M1,L2M2,,LnMn are line segments parallel to BCandM1,M2,,Mn are on AC, then the sum of the lengths of L1M1,L2M2,,LnMn is a(n+1)2 b. a(n−1)2 c. an2 d. none of these
View Solution