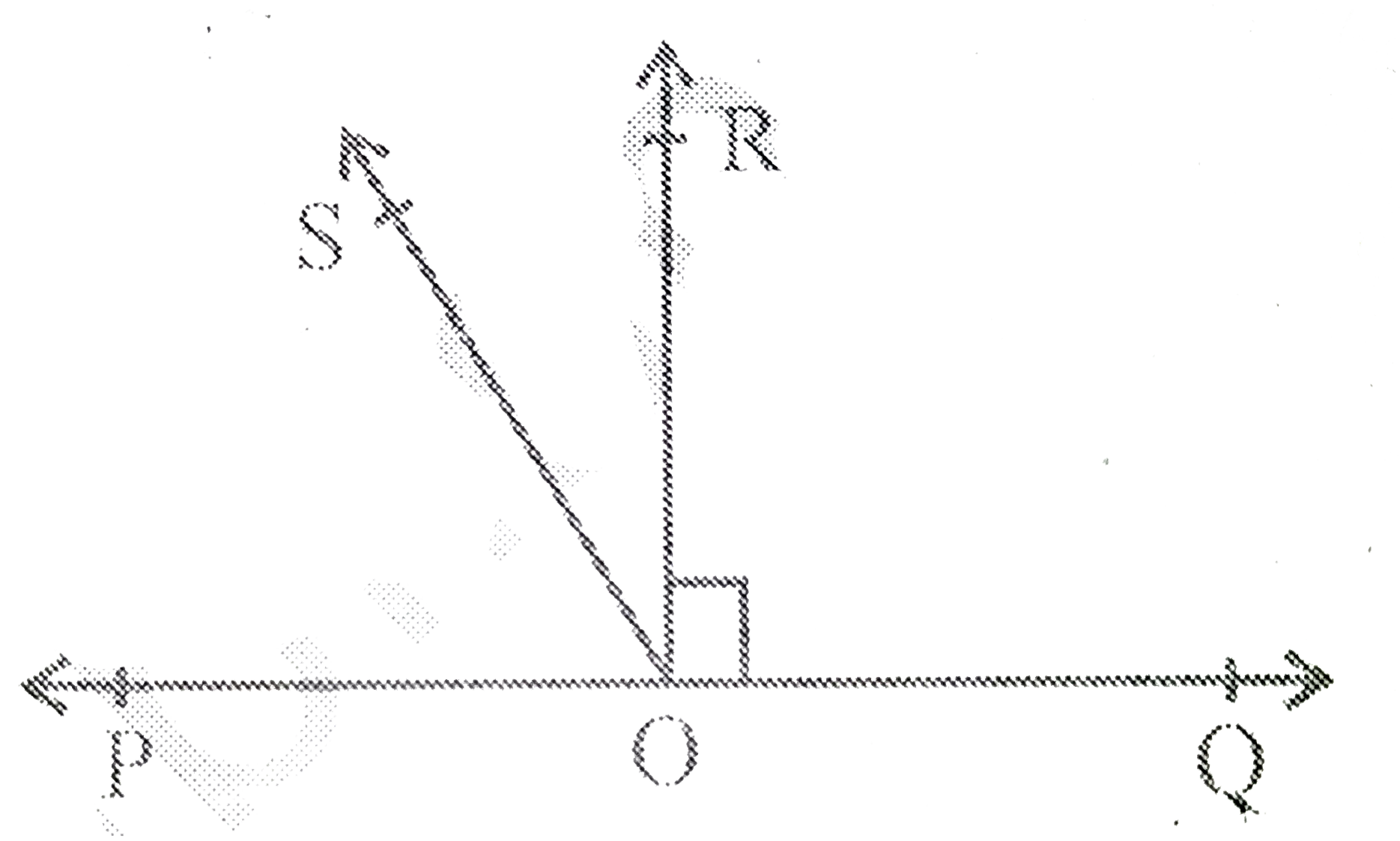
In Figure, ray OS
stand on a line POQ.
Ray OR
and ray OT
are angle bisectors of ∠POS and ∠SOQ
respectively. If ∠POS=x,
find ∠ROT

Step by step video & image solution for In Figure, ray O S stand on a line P O Qdot Ray O R and ray O T are angle bisectors of /_P O S\ a n d\ /_S O Q respectively. If /_P O S=x , find /_R O T by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
The number of S-O-S and O-H links in H2S2O7 molecule are respectively
A0,2B1,2C2,2D2,1The I.P1's of N,P,O & S are in the order of
AS>P<O>NBN>O>P>SCN>O<P>SDN<O<P<S
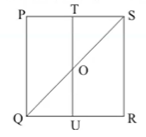
In Figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR . Find the area of OTS if PQ=8 cm.
View SolutionIn Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS=12(∠QOS−∠POS).
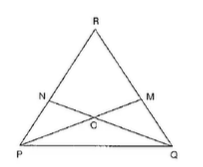
View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
View SolutionABCD is a parallelogram whose AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar ( POA)= ar ( QOC).
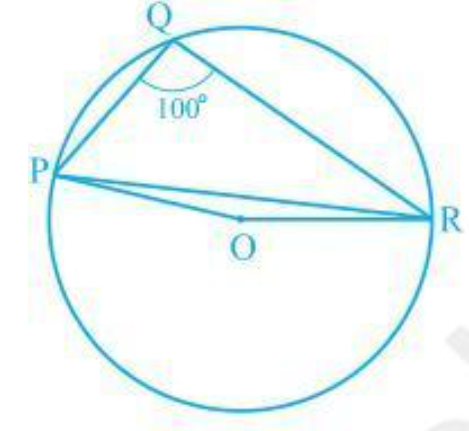
View SolutionIn Fig. 10.37, ∠PQR = 100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR.
View SolutionLet O be the origin, and OX,OY,OZ be three unit vectors in the direction of the sides QR , RP , PQ , respectively of a triangle PQR. |OX×OY|= s∈(P+R) (b) sin2R (c)sin(Q+R) (d) sin(P+Q).
View Solution
