ABCD is a parallelogram. P is the mid-point of AB.BD and CP intersect at Q such that CQ:QP=3:1. If ar (PBQ)=10 cm2, find the area of parallelogram ABCD
Let CQ=3x and PQ=x
ar(△PBQ)=10cm2
As we know that, Area of triangle = 12×Base×Height
Area (△PBQ) = 12×X×h
X×h=20
Area of △BQC=12×3X×h
=12×3×20
=30cm2
Now, area of △PCB=12×PB×H=30cm2
PB×H=60cm2
As we know that area of ∣∣gm = Base×Height
Area(ABCD)=AB×H=2BP×H
Area(ABCD)=120cm2
Hence, area of∣∣gm ABCD is 120cm2.
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionPQRS is a trapezium having PS a n d QR as parallel sides. A is any point on PQandB is a point on SR such that ABQR . If area of PBQ is 17cm2, find the area of ASR
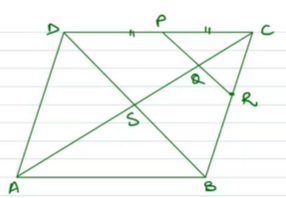
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R, prove that R is a mid-point of BC
View SolutionP is any point on base BC of ABC and D is the mid-point of BC.DE is drawn parallel to PA to meet AC at E. If ar(ABC)=12cm2 , then find area of EQC
View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(△POA)=ar(△QOC).
View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
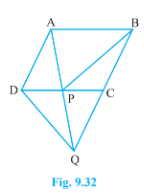
View SolutionIn Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such thatAD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
View SolutionIn A ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (RQC)=38 ar ( ABC)
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
View Solution