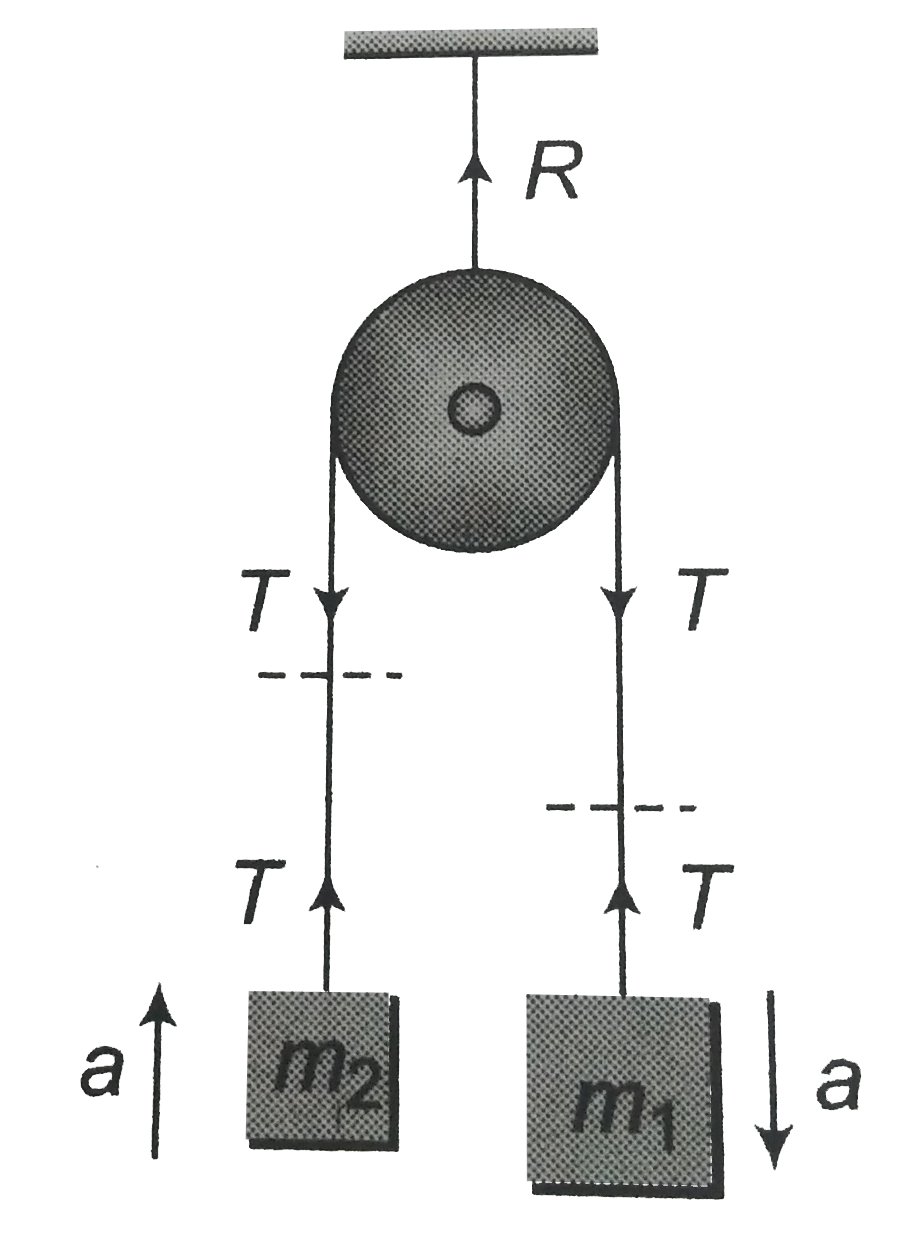
In the arrangement shown, find the acceleration of each block, tension in the string and reaction in the pulley. The string and pulley are light (massless) (m1>m2). Neglect the friction in pulley.

Video Solution
Text Solution
Since m2>m1, the block of mass m1 will move downward and the block of mass m2, upward.
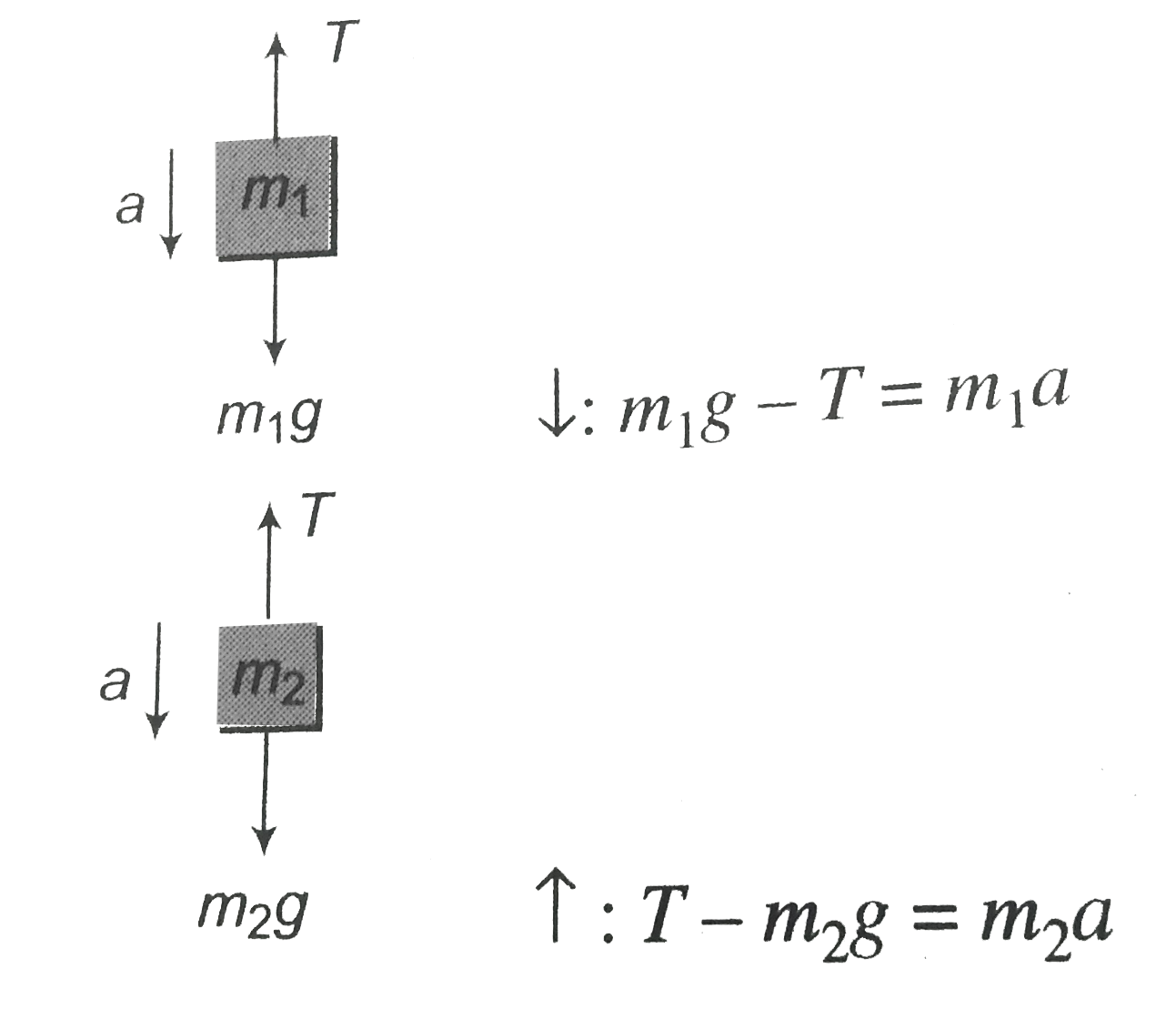
↓:m1g−T=m1a (i)
↑:T−m2g=m2a (ii)
Solving (i) and (ii), we get
a=(m1−m2)g(m1+m2)
T=2m1m2gm1+m2
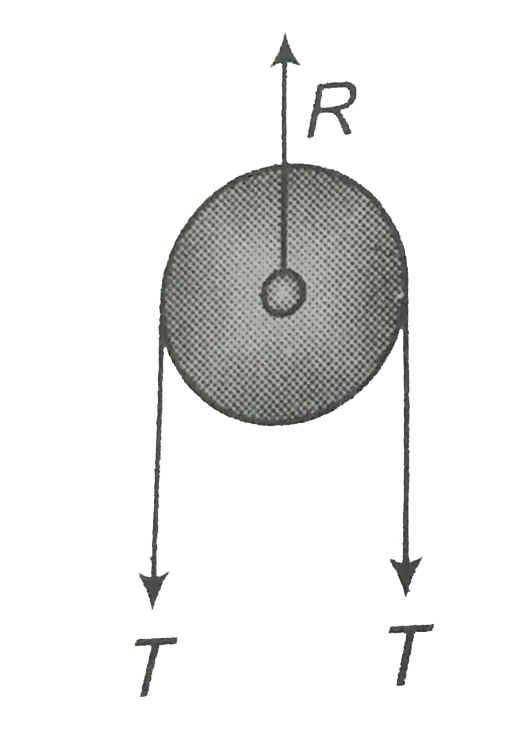
R−2T=0 [since the pulley is massless]
where R is the reaction in the pulley.
|
Similar Questions
Knowledge Check
The tension in the string in the pulley system shown in
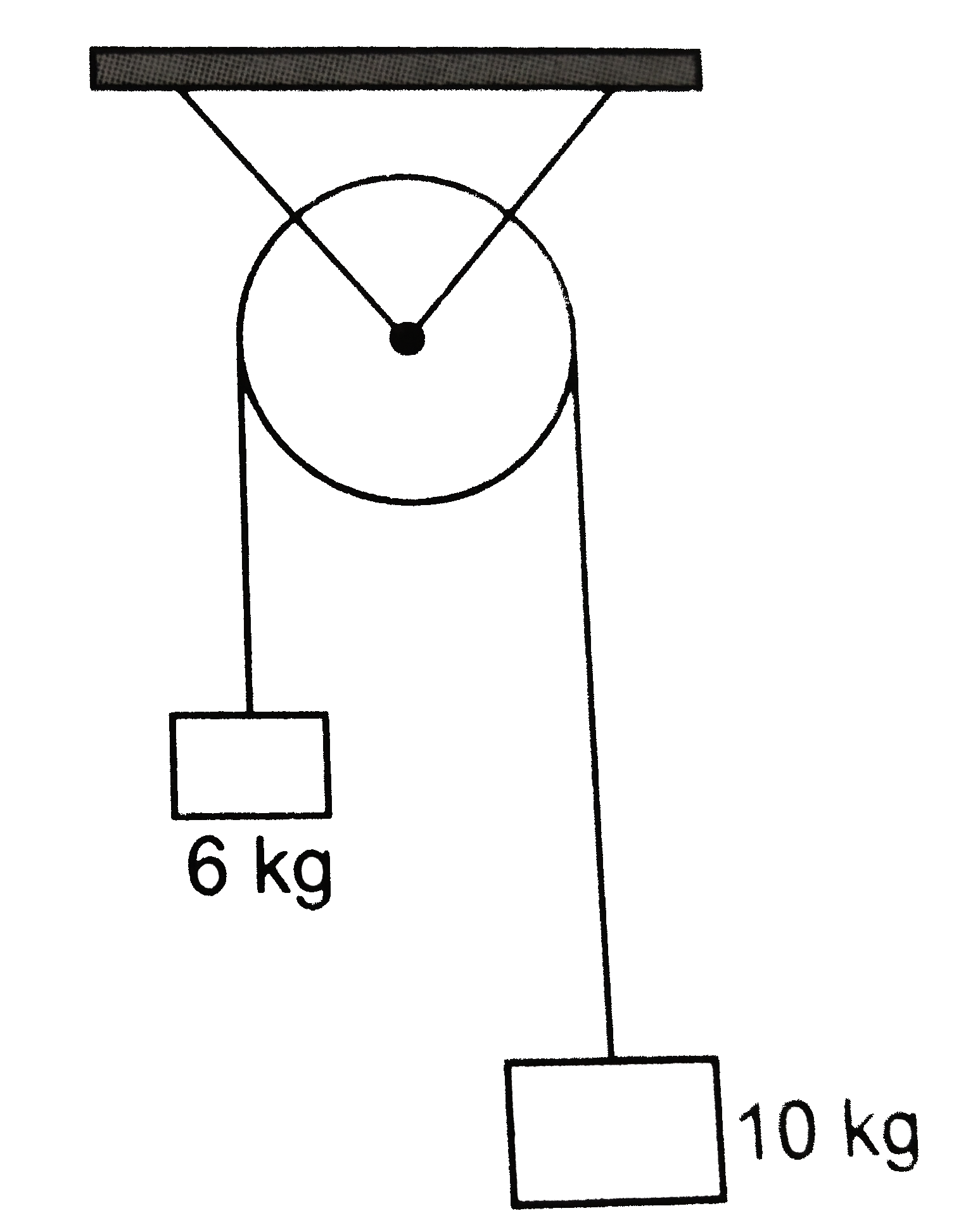 .A5.7NB7NC7.5ND73.5N
.A5.7NB7NC7.5ND73.5NThe acceleration of the block (A) and (B) respectively in situation shown in the figure is: (pulleys and string are massless).
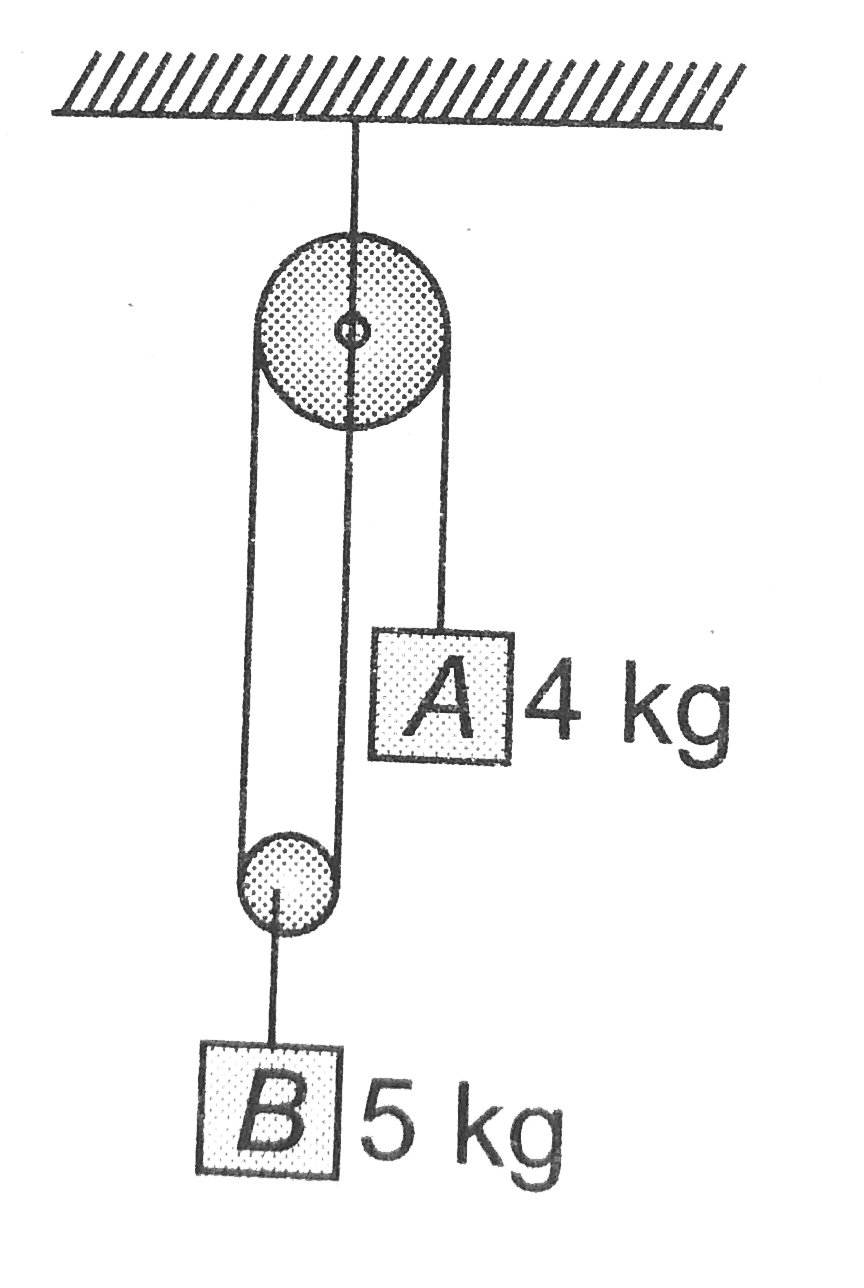 A2g7 downward, g7 upwardB2g3 downward, g3 upwardC1013g downward, 5g13 upwardDnone of these
A2g7 downward, g7 upwardB2g3 downward, g3 upwardC1013g downward, 5g13 upwardDnone of theseIn the arrangement shown, the pulleys and strings are massless. The acceleration of block B is :
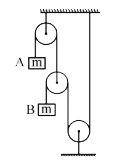 Ag/2B5g/3C2g/3D2g/5
Ag/2B5g/3C2g/3D2g/5
In the arrangement shown, inclined plane is smooth, strings and pulleys are massless. Find T1T2
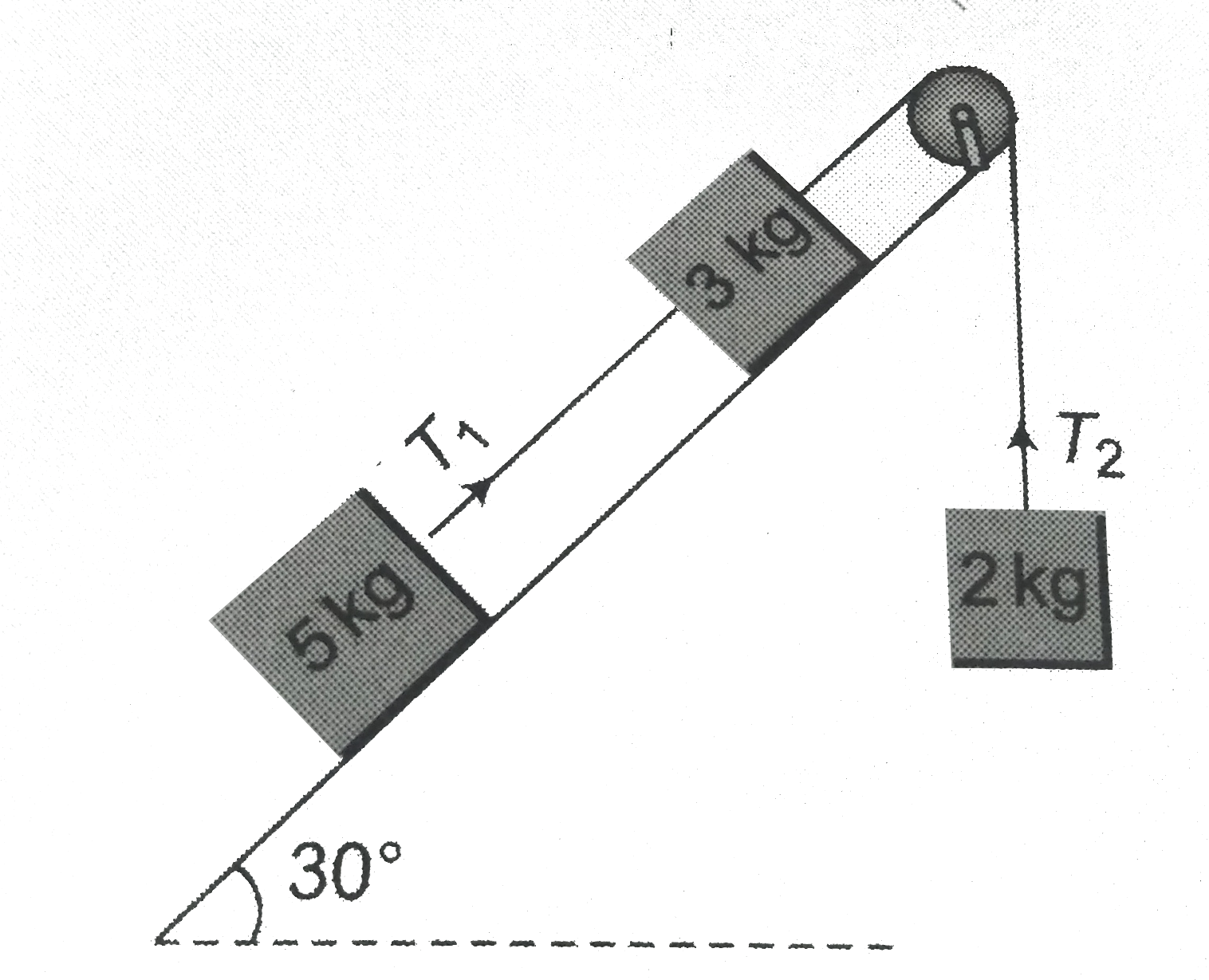
View SolutionFor the arrangement shown in figure, angle θ for which tension T1 in the left string will be minimum is (Pulley and strings are ideal)

View SolutionIn the arrangement shown, the pulleys and the strings are ideal.The acceleration of the block B is
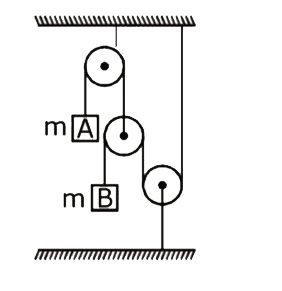
View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.

View SolutionIn the arrangement shown, the pulleys and the string are ideal. The acceleration of block B is.

View Solution



