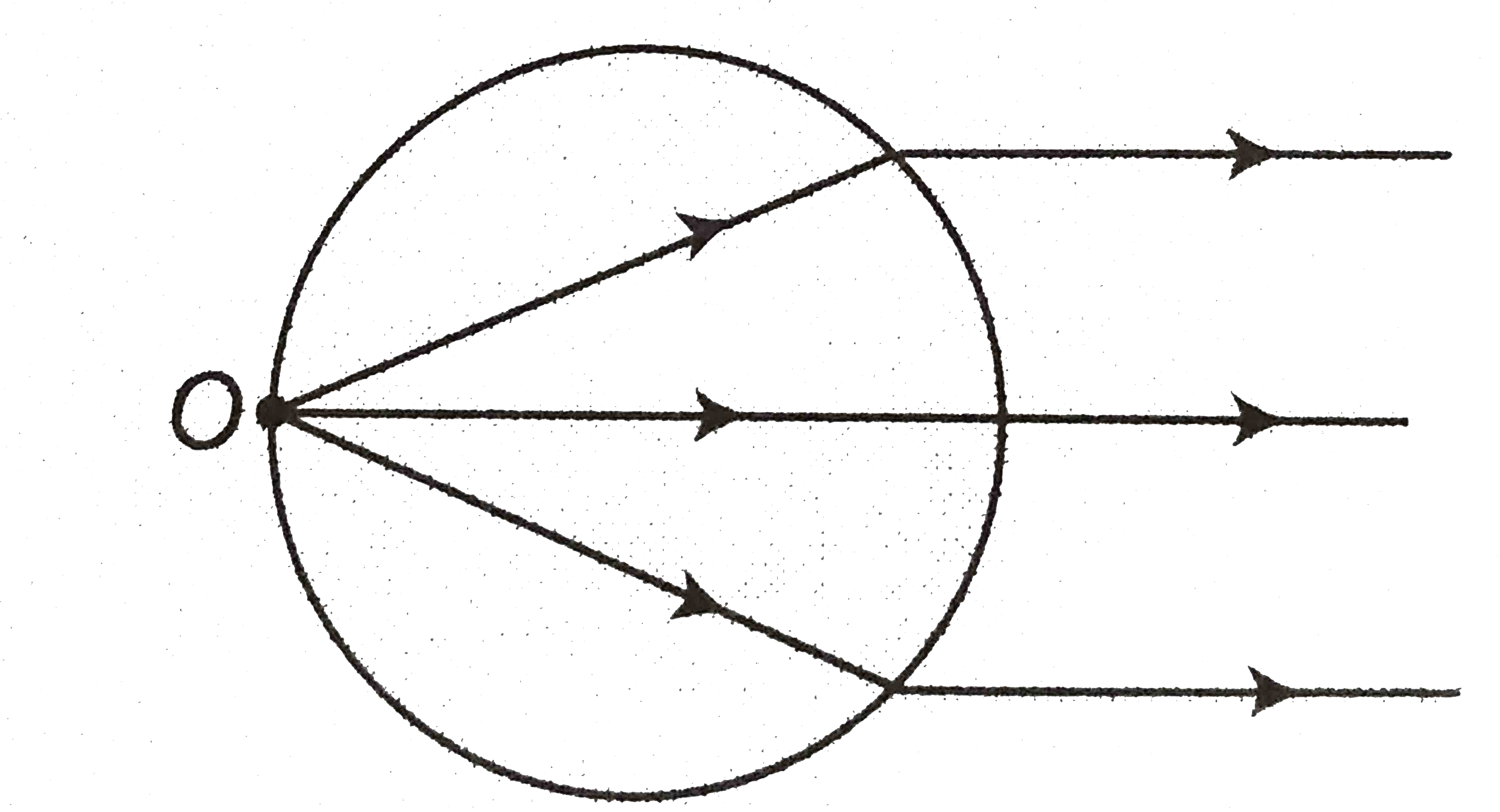
An object O is stuck on the surface of a transparent solid spher of radius 20 cm. Find refractive index of the sphere such that rays from the object after refraction from the opposite side emerge as a parallel beam, as shown Also prove that refractive index has the same value in the given situation for any value of radius of sphere.
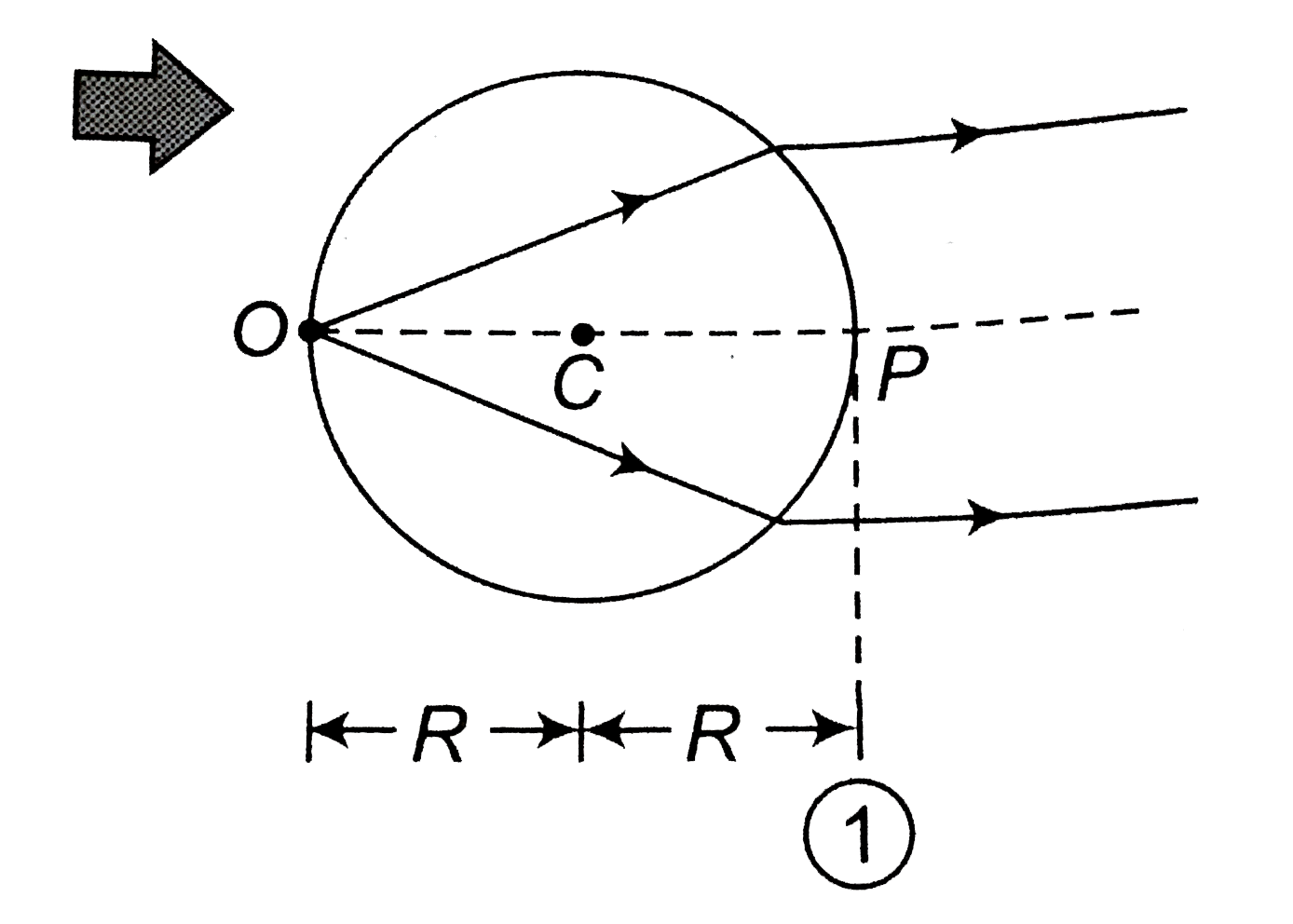
Refraction at 1:
μ1=μ,μ2=1,u=−2R,v=∞,R=−R
μ2v−μ1u=μ2−μ1R
1∞−μ−2R=1−μR
μ2R=μ−1R
μ=2μ−2
μ=2.0
Refractive index is μ=2, for any value of R.
Similar Questions
A ray of light falls on a transparent sphere with centre at C as shwon in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is
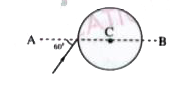
View SolutionA ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

View SolutionA ray of light falls on a transparent sphere with centre at C as shwon in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

View SolutionA ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

View SolutionA parallel beam falls on solid glass sphere of radius R and refractive index mu . What is the distance of final image after refraction from two surfaces of sphere? What is, the condition for the image to be real?
View SolutionA ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

View SolutionParallel rays of light are falling on convex sphere surface of radius of curvature R = 20 cm as show. Refractive index of the medium is μ=1.5. A refraction from the spherical surface parallel rays

View SolutionA parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
View Solution

