Evaluate [i14−(1i)34]2
The correct Answer is:0
To evaluate the expression (i14−(1/i)34)2, we will follow these steps:
Step 1: Simplify i14
We know that i is the imaginary unit, defined as i=√−1. The powers of i cycle every 4:
- i1=i
- i2=−1
- i3=−i
- i4=1
To find i14, we can reduce the exponent modulo 4:
14mod4=2
Thus,
i14=i2=−1
Step 2: Simplify (1/i)34
We can rewrite 1i as −i (since 1i⋅i=1). Therefore,
(1/i)34=(−i)34
Now, we simplify (−i)34. The powers of −i also cycle every 4:
- (−i)1=−i
- (−i)2=−1
- (−i)3=i
- (−i)4=1
Now, we find 34mod4:
34mod4=2
Thus,
(−i)34=(−i)2=−1
Step 3: Substitute back into the expression
Now we substitute back into our original expression:
i14−(1/i)34=−1−(−1)=−1+1=0
Step 4: Square the result
Now we square the result:
(i14−(1/i)34)2=02=0
Final Answer
Thus, the final answer is:
0
We know that i is the imaginary unit, defined as i=√−1. The powers of i cycle every 4:
- i1=i
- i2=−1
- i3=−i
- i4=1
14mod4=2
Thus,
i14=i2=−1
We can rewrite 1i as −i (since 1i⋅i=1). Therefore,
(1/i)34=(−i)34
Now, we simplify (−i)34. The powers of −i also cycle every 4:
- (−i)1=−i
- (−i)2=−1
- (−i)3=i
- (−i)4=1
34mod4=2
Thus,
(−i)34=(−i)2=−1
Now we substitute back into our original expression:
i14−(1/i)34=−1−(−1)=−1+1=0
Now we square the result:
(i14−(1/i)34)2=02=0
Thus, the final answer is:
0
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - AAKASH INSTITUTECHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - Assignment (Section -A) (objective Type Questions ( one option is correct)
47 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - AAKASH INSTITUTECHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - Assignment (Section -B) (objective Type Questions ( one option is correct)
78 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - AAKASH INSTITUTECHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - section-J (Aakash Challengers Qestions)
16 Videos
- BINOMIAL THEOREMBOOK - AAKASH INSTITUTECHAPTER - BINOMIAL THEOREMEXERCISE - Assignment (section-J) Objective type question (Aakash Challengers Questions)
4 Videos
- CONIC SECTIONSBOOK - AAKASH INSTITUTECHAPTER - CONIC SECTIONSEXERCISE - SECTION - J ( Aakash Challengers Questions )
14 Videos
Similar Questions
The value of i−9999 is
View SolutionThe solution of the equation z(¯¯¯¯¯¯¯¯¯¯z−3i)=2(2+3i) is/are
View SolutionLet n be even postiive integer such that n2 is odd and let α0,α1,……..,αn+1 be the complex roots of unity of order n. prove that n1IIk=0(a+bα2k)=(αn2+bn2)2 for any complex numbers a and b
View SolutionFor any natural number n, the number A given by A=2903n−803n−464n+261n is divisible by
View SolutionThe angle between the tangent drawn from origin to the circle (x−7)2+(y+1)2=25 is :
View Solution{i^(17)-((1)/(i))^(34)}^(2)
View Solutionइन को सरल करे |
{i17−(1i)34}2
View Solutionचित्र में ज्ञात कीजिये (i) देहली आवर्ती (ii) पर्दार्थ का कार्यफलन
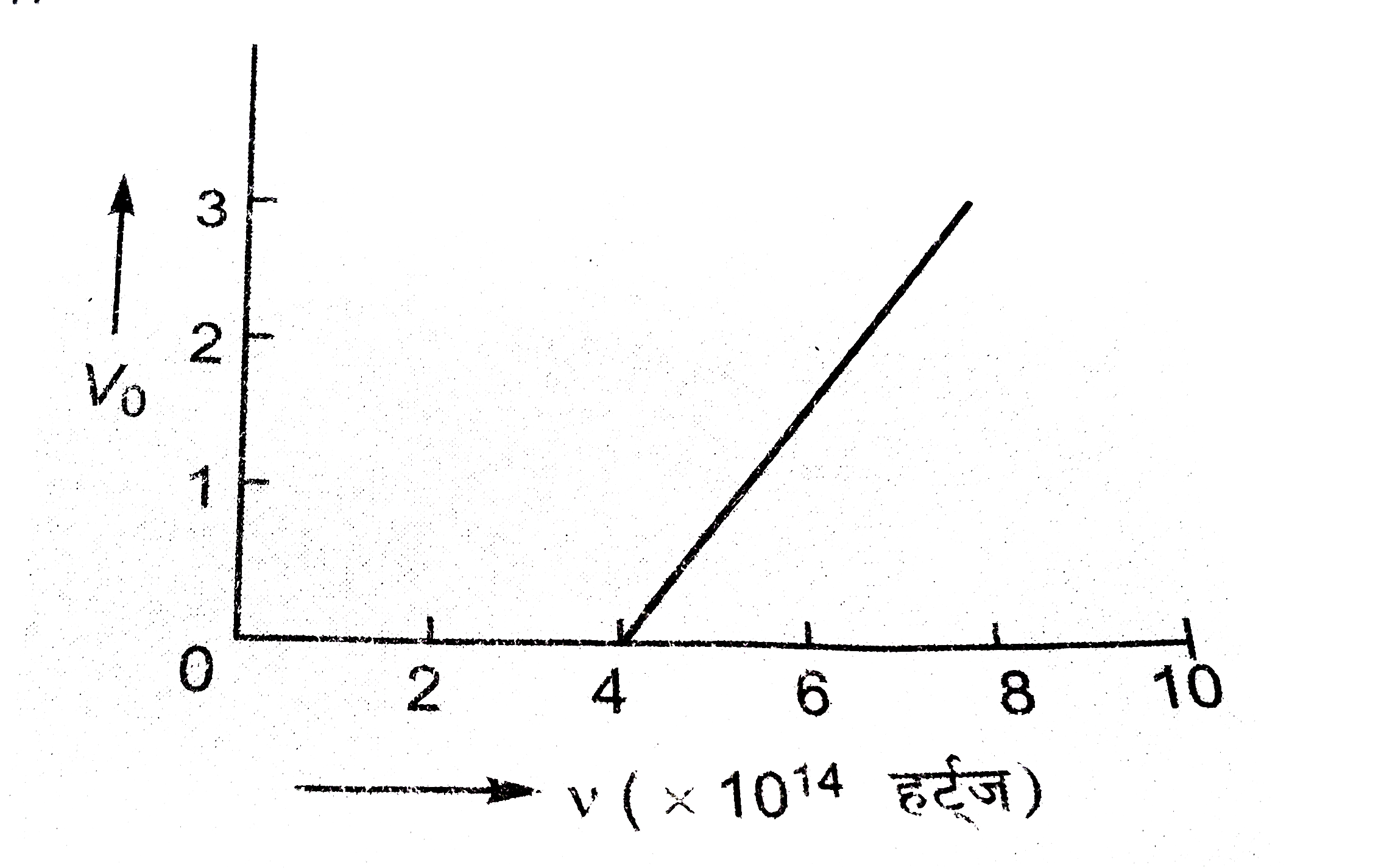
(ii) W=hv0=6.6×10−34×4×10−14
=6.6×10−34×4×10141.6×10−19
View Solutionयदि a2+1a2=34, निम्न के मान ज्ञात कीजिए ।
(i) a+1a
(ii) a−1a
View Solutionमान निकालें
[i17−(1i)34]2
View Solutionಇವುಗಳ ಮೊತ್ತ ಕಂಡುಹಿಡಿಯಿರಿ. (i) 7+1012+14+ ....+ 84
View Solutionಇವುಗಳ ಮೊತ್ತ ಕಂಡುಹಿಡಿಯಿರಿ. (i) 34+32+30+ ....+10
View Solutionদেখাও যে, [i17−(1i)34]2=2i
View Solution[i17−(1i)34]2=2i.
View Solutionagreed i^2=-1 If so (i^10 - 1/i^11) +(i^11 - 1/i^12)+(i^12 - 1/i^13)+(i^13 -1/i^14)+(i^14-1/i^15) =
View Solution

