In the figure (i) a disc of mass M(kg) and radius R(m) is rotating smoothly about a fixed vertical axis AB with angular speed 26rad/s A rod rod CD of length R2(m) and mass M(kg) is hinged at one end at point 'D' on the disc. The rod remains in vertical position and rotates along with the disc about axis AB. At some moment the rod CD gets a very smal impulse at point 'C' due to air due to which the rod falls on the disc along one radius and sticks to the disc as shown in figure (ii). Now find the angular velocity of the disc in rad/s.

The correct Answer is:36
MI of the system when rod is vertical
I=12mR3+mR2
MI of system when rod is horizontal
I'=12mR2+⎡⎢
⎢
⎢⎣m(R2)212+m(3R4)2⎤⎥
⎥
⎥⎦
=1312mR2
from conservation of angular momentum of system about axis AB is
Iω=I'ω'
or ω'=32mR2ω1312mR2=1813ω
Similar Questions
Knowledge Check
A homogeneous disc of mass 2 kg and radius 15 cm is rotating about its axis with an angular velocity of 4 rad/s. the linear momentum of the disc is
A1.2 kg m/sB1.0 kg m/sC0.6 kg m/sDzeroA rod AB of mass m and length l is rotating about a vertical axis as shown. It's moment of inertia about this axis is :
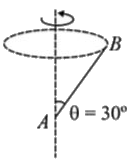 Aml23Bml24Cml216Dml212
Aml23Bml24Cml216Dml212A mechanism consists of a part which is translated with a velocity u and a rod AB of length L and mass M hinged at A The rod rotates about axis A with angular velocity ω the kinetic energy of rod when it is vertical as shown is
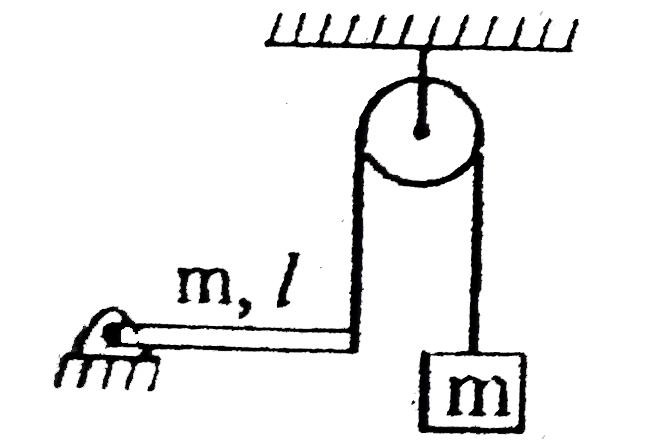 A12Mu2+16ML2ω2B12Mu2+16MLωuC12Mu2+16ML2ω2+12MLωuDnone of these
A12Mu2+16ML2ω2B12Mu2+16MLωuC12Mu2+16ML2ω2+12MLωuDnone of these
A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
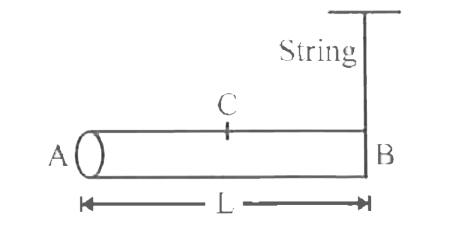
View SolutionThe moment of inertia of a thing uniform rod of length L and mass M, about axis CD (as shown in figure) is

View SolutionA uniform rod AB of length L and and weight Mg is hinged at one end A. The rod is kept in the horizontal position by a massless string. If the string is cut, then the angular acceleration of the rod will be
[M.I. of the rod about A is ML23]
View SolutionA uniform disc of mass M and radius R is rotating freely about its central vertical axis with angular speed w0. Another disc of mass m and radius r is free to rotate about a horizontal rod AB. Length of the rod AB isL(<R) and its end A is rigidly attached to the vertical axis of the first disc. The disc of mass m, initially at rest, is placed gently on the disc of mass M as shown in figure. Find the time after which the slipping between the two discs will cease. Assume that normal reaction between the two discs is equal to mg. Coefficient of friction between the two discs is μ.

View SolutionA rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View Solution


