A rectangular box with an open top is constructed from cardboard to have a square base of area x2 and height h. If the volume of this box is 50 cubic units, how many square units of cardboard in terms of x, are needed to build this box ?
5x2
6x2
200x+x2
200x+2x2
The correct Answer is:C
Use the given volume = 50 to get h in terms of x :
Volume = length × width × height
50=x.x.h
h=50x2
The area you're looking for is equal to four lateral faces and one bottom face.
Each lateral face has are xh=x50x2=50x, and the base has area x2, so the total area you're looking for is
4(50x)+x2=200x+x2
Similar Questions
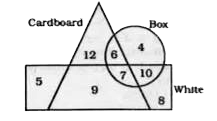
In the given figure, how many cardboard boxes are not white?
View SolutionThe volume of a box is 13400 cubic cm. The area of its base is 670 square cm. Find the height of the box.
View SolutionAn open box with a square base is to be made out of a given quantity of card board of area c2 square units. Show that the maximum volume of the box is c36√3 cubic units.
View SolutionAn open box with a square base is to be made out of a given quantity of card board of area c2 square units. Show that the maximum volume of the box is c36√3 cubic units.
View SolutionOR An open box with a square base is to be made out of a given quantity of cardboard of area c2 square units. Show that the maximum volume of the box is c36 √3 cubic units.
View Solutionवर्गाकार आधार वाला एक खुला बॉक्स, a2 वर्ग इकाई क्षेत्रफल के लकड़ी के गट्टे की दी गई मात्रा द्वारा बनाया जाता है। बॉक्स के आयतन के महत्तम होने के लिए बॉक्स की विमाएँ ज्ञात कीजिये। साथ ही, महत्तम आयतन भी ज्ञात कीजिये।
View SolutionFrom the four corners of a rectangular cardboard 38cm×26cm square pieces of size 3 cm are cut and the remaining cardboard is used to form an open box. Find the capacity of the box formed.
View SolutionSixteen cylindrical cans each with a radius of 1 unit are placed inside a cardboard box four in a row. If the cans touch the adjacent cans and or the walls of the box, then which of the following could be the interior area of the bottom of the box in square units ?
View Solution
