There is a hollow cylinder of radius R and it is rotating with constant angular speed ω. There is a point mass which rotates along with the cylinder and geta carried upward. Friction is enough such that the point mass does not slip with respect to the cylinder as long as the normal force is becomes zero. If the path of the particle after it lost contact with the cylinder is as shown in the figure then,

In Order to happen this where most the particle lose contact with the cylinder?
h=R2
h=R√3
h=R√2
h=R√π
The correct Answer is:C
12gsinθ.4v2g2cos2θ=2R……..(1)

v2=Rgsinθ……(2)
From (1) and (2) tanθ=1
Similar Questions
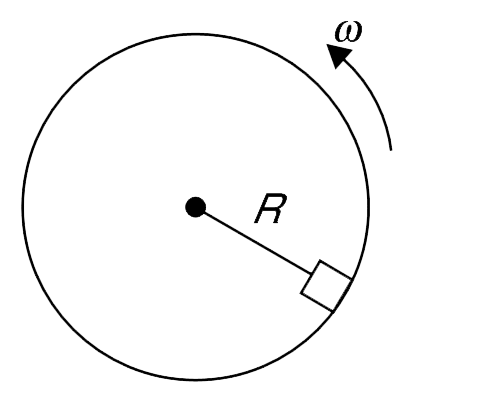
A cylinder with radius R spins about its horizontal axis with angular speed ω. There is a small block lying on the inner surface of the cylinder. The coefficient of friction between the block and the cylinder is μ. Find the value of ω for which the block does not slip, i.e., stays at rest with respect to the cylinder.
View SolutionAn infinite cylinder of radius r with surface charge density σ is rotated about its central axis with angular speed ω. Then the magnetic field at any point inside the cylinder is
View Solution
Knowledge Check
There is a hollow cylinder of radius R and it is rotating with constant angular speed ω. There is a point mass which rotates along with the cylinder and geta carried upward. Friction is enough such that the point mass does not slip with respect to the cylinder as long as the normal force is becomes zero. If the path of the particle after it lost contact with the cylinder is as shown in the figure then,

What is the value of ω (in terms of g and R)A√g√3RB√g2√πRC√g2RD√g√2RA solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2Three identical cylinders of radius R are in contact.Each cylinder is rotating with angular velocity ω.A thin belt is moving without sliding on the cylinders. Calculate the magnitude of velocity of point P with respect to Q.P and Q are two points of belt which are in contact with the cylinder.
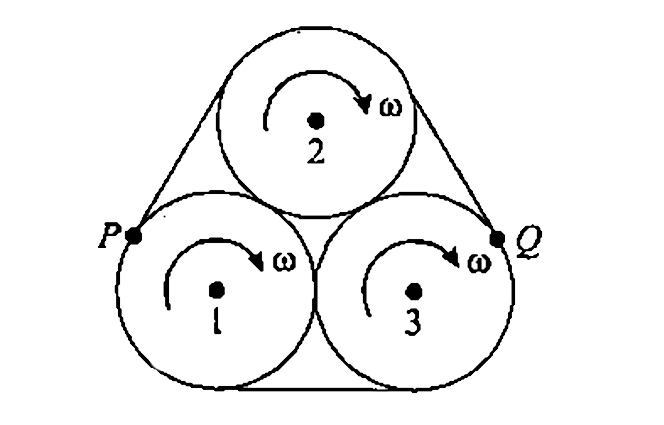 A2RωBRωCRω/2DRω/√3
A2RωBRωCRω/2DRω/√3
A cylinder of radius R full of liquid of density p is rotated about its axis at w rad/s. The increase in pressure at the centre of the cylinder will be
View SolutionA solid cylinder of mass 'M' and radius 'R' is rotating along its axis with angular velocity ω without friction. A particle of mass 'm' moving with velocity v collides aganist the cylinder and sticks to its rim. After the impact calculate angular velocity of cylinder .
View SolutionAn solid cylinder of mass 20kg and radius 20cm rotates about its axis with a angular speed 100rads−1. The angular momentum of the cylinder about its axis is.
View SolutionA hollow vertical cylinder of radius R is rotated with angular velocity ω about an axis through its centre. What is the minimum coefficient of static friction between block M and cylinder wall necessary to keep the block suspended on the inside of the cylinder ?
View SolutionA hollow cylinder of radius R rotates about its axis which is vertical. A block remains in contact with the inner wall if the frequency of rotation is f hertz, but falls at lower frequaencies. The coefficient of friction between the block and the cylinder is
View Solution

