Consider two complex number z and ω satisfying |z|=1 and |ω−2|+|ω−4|=2. Then which of the following statements(s) is (are) correct?
Re(zω) can never exceed 4
If argz=argω,then |z+2|is equal to 3
The minimum value of |z−ω| to equal to 2
The maximum value of |z−ω| is equal to 6
The correct Answer is:B
z lies on a unit circle centred at origin and ω lies on the line segment joining (2,0)&(4,0)
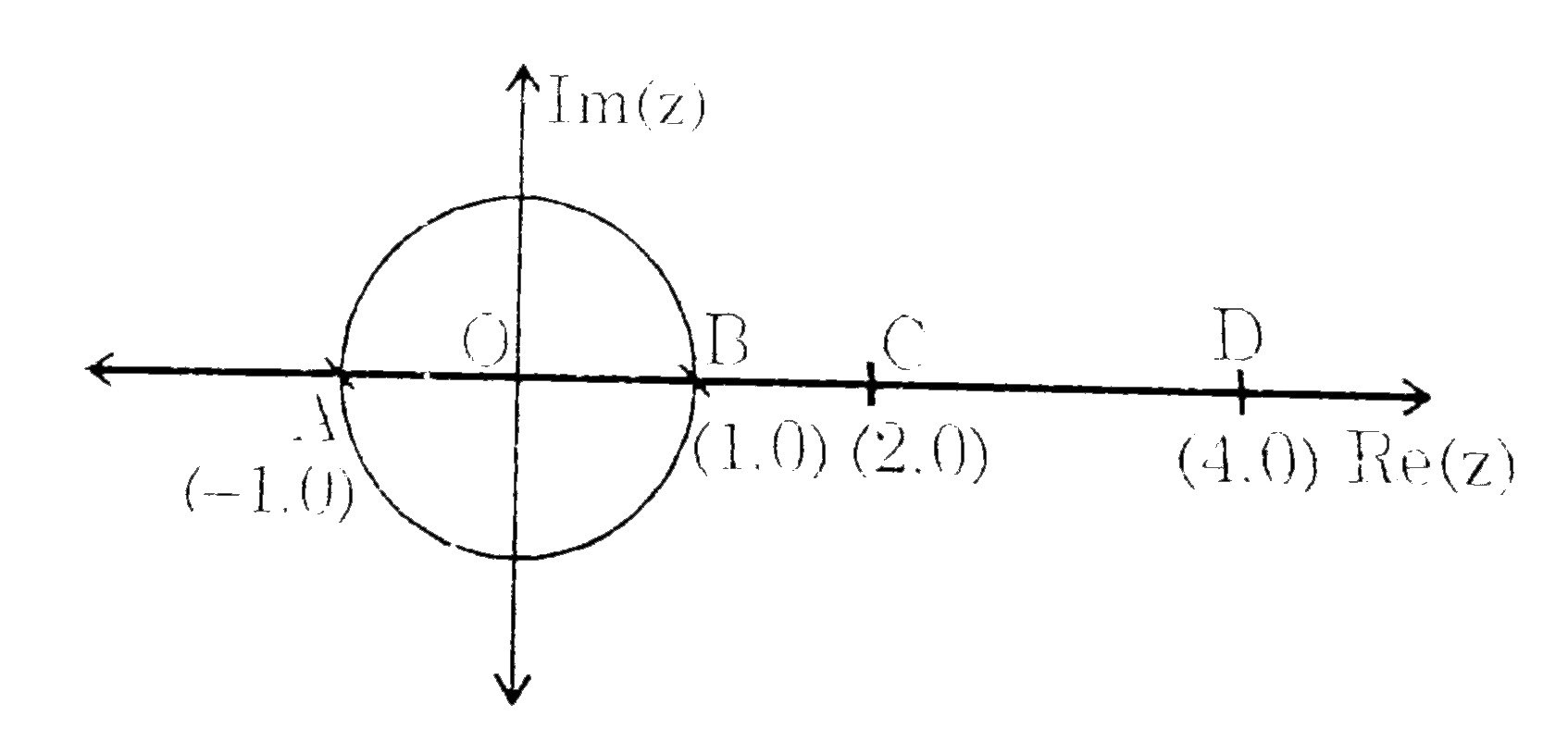
∴|z−ω|minimum=BC=1
&|z−ω|maximum=AD=5
Let z=eiθ⇒zω==ωeiθ
where ω>0
⇒Re(zω)=ωcosθ≤4
As argω=0⇒argz=0
⇒zlines atB(1,0)
∴|z+2|=|1+2|=3
Topper's Solved these Questions
Similar Questions
Knowledge Check
Suppose z and ω are two complex number such that |z+iω|=2. Which of the following is ture about |z| and |ω|?
A|z|=|ω|=12B|z|=12,|ω|,|ω|=34C|z|=|ω|=34D|z|=|ω|=1Consider the two complex numbers z and w, such that
w=z−1z+2=a+ib, where a,b∈R and i=√−1.
Which of the following equals to |z|?A|w|B(a+1)2+b2Ca2+(b+2)2D(a+1)2+(b+1)2Consider the two complex numbers z and w, such that
w=z−1z+2=a+ib, where a,b∈R and i=√−1.
Which of the following is the value of −ba, whenever it exists?A3tan(θ2)B13tan(θ2)C−13cotθD3cotθ2
If z1=a+ibandz2=c+ are complex numbes such that |z1|=|z2|=1andRe(z1¯z2)=0 then the pair of complex numbers ω1=a+icandω2=b+ satisfy which of the following relations? (A) |ω1|=1 (B) |ω2|=1 (C) Re(ω1¯¯ω2)=0 (D) Im(ω1¯¯ω2)=0
View SolutionLet z and ω be two complex numbers such that |z|≤1,|ω|≤1 and |z−iω|=|z−i¯¯ω|=2, then z equals (a)1ori (b). ior−i (c). 1or−1 (d). ior−1
View SolutionConsider the two complex numbers z and w, such that
w=z−1z+2=a+ib, where a,b∈R and i=√−1.
If z=CiSθ, which of the following does hold good?
View SolutionSuppose z and ω are two complex number such that |z|≤1 , |ω|≤1 and |z+iω|=|z−i¯¯ω|=2 The complex number of ω can be
View SolutionLet Z and w be two complex number such that |zw|=1 and arg(z)−arg(w)=π/2 then
View Solution
