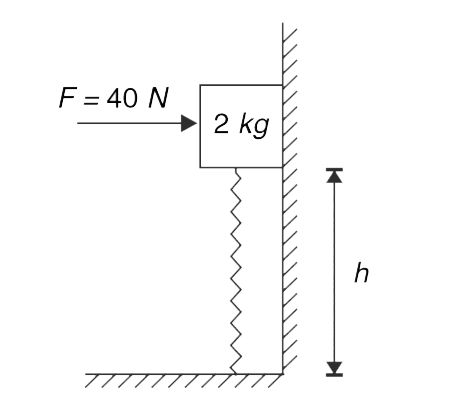
(i) In the arrangement shown in the figure the coefficient of friction between the 2 kg block and the vertical wall is μ=0.5. A constant horizontal force of 40 N keeps the block pressed against the wall. The spring has a natural length of 1.0 m and its force constant is k=400Nm–1. What should be the height h of the block above the horizontal floor for it to be in equilibrium. The spring is not tied to the block.
(ii) A block of mass M is pressed against a rough vertical wall by applying a force F making an angle of θ with horizontal (as shown in figure). Coefficient of friction between the wall and the block is μ=0.75.
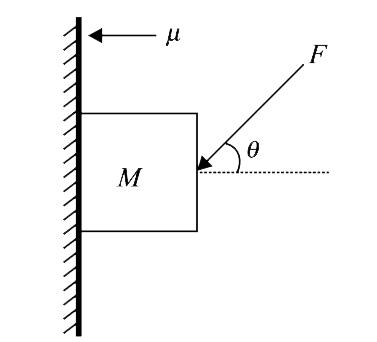
(a) If F = 2 Mg, find the range of values of θ so that the block does not slide
[Take tan37∘=0.75,sin24∘=0.4]
(b) Find the maximum value of θ above which equilibrium is not possible for any magnitude of force F.
The correct Answer is:θ≤13∘
37∘
Topper's Solved these Questions
Similar Questions
A block of mass 4kg pressed againest a rought wall by two perpendicular horizontal forces F1andF2as shown in figure Coefficient of static friction between the block and wall is 0.6 and that of kinetic friction is 0.5

For the data of Q 28 ,Find the magnitude of acceleration of the block
View SolutionA block is pressed towards a vertical wall using a horizontal force equal to n times its weight which prevents the block from sliding down.Then coefficient of static friction between the block and the wall is?
View Solution
Knowledge Check
In the arrangement shown in figure coefficient of friction between 5kg block and incline plane is μ=0.5. Friction force acting on the 5kg block is
 A20NB15NC10ND5N
A20NB15NC10ND5NIn the arrangement shown in figure the wall is smooth and friction coefficient between the blocks is μ=0.1. A horizontal force F=1000N is applied on the 2kg block. The wrong statement is :
 AThe normal interaction force between the blocks is 1000N.BThe friction force between the blocks is zero.CBoth the blocks accelerate downward with acceleration gm/s2DBoth the blocks remain at rest
AThe normal interaction force between the blocks is 1000N.BThe friction force between the blocks is zero.CBoth the blocks accelerate downward with acceleration gm/s2DBoth the blocks remain at restA block of mass 2kg is held at rest against a rough vertical wall by passing a horizontal (normal) force of 45N. Coefficient of friction between wall and the block is equal to 0.5. Now a horizontal force of 15N (tangential to wall) is also applied on the block. Then the block will :
AMove horizontally with acceleration of 5m/s2BStart to move with an acceleration of magnitude 1.25m/s2CRemain stationaryDStart to move horizontally with acceleration greater than 5m/s2
A block of weight 5 N is pushed against a vertical wall by a force 12 N . The coefficient of friction between the wall and block is 0.6 . Find the magnitude of the force exerted by the wall on the block :
View SolutionA block of mass 4kg pressed againest a rought wall by two perpendicular horizontal forces F1=300NandF2=100Nas shown in figure Coefficient of static friction between the block and wall is 0.6 and that of kinetic friction is 0.5
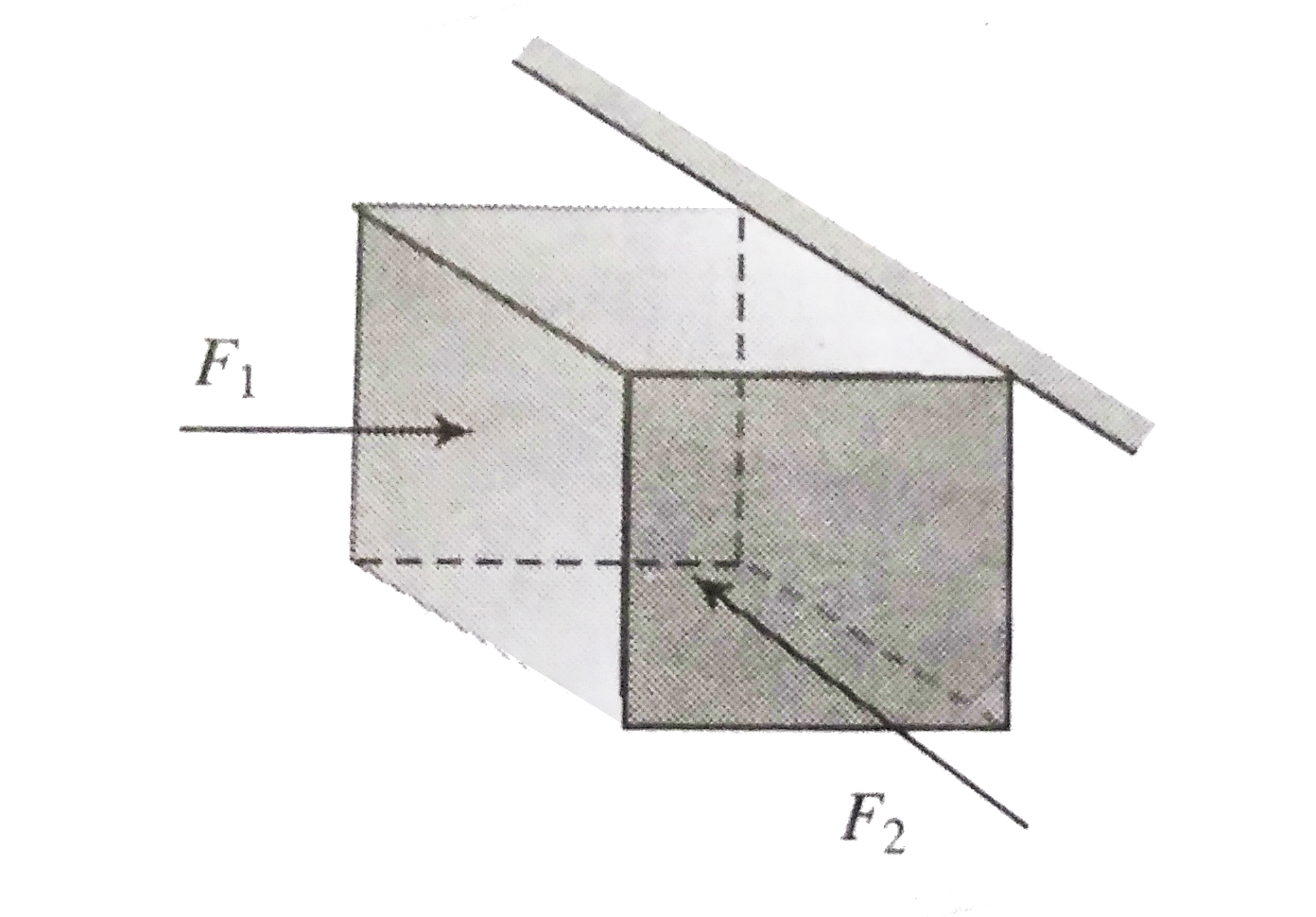
For the above data, what is the acceleration of block?
View SolutionA block of mass 4kg pressed againest a rought wall by two perpendicular horizontal forces F1andF2as shown in figure Coefficient of static friction between the block and wall is 0.6 and that of kinetic friction is 0.5

For the data of Q 28 ,Find the magnitude of acceleration of the block
View SolutionA block of mass 4kg pressed againest a rought wall by two perpendicular horizontal forces F1andF2as shown in figure Coefficient of static friction between the block and wall is 0.6 and that of kinetic friction is 0.5

For the above data, what is the acceleration of block?
View SolutionA block of weight 5 N is pushed against a vertical wall by a force 12 N . The coefficient of friction between the wall and block is 0.6 . Find the magnitude of the force exerted by the wall on the block :

View Solution

