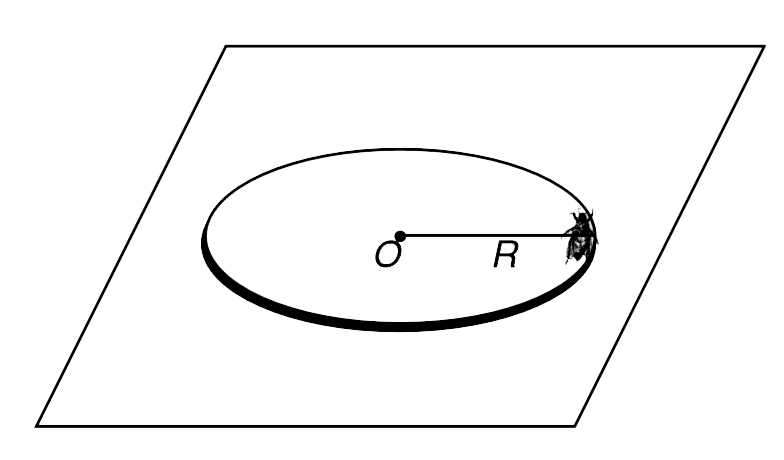
A small body of mass m is at rest inside a narrow groove carved in a disc. Groove is a circle of radius R concentric to the disc. Mass of the disc is also m . The disc lies on a smooth horizontal floor. The small body is given a sharp impulse so that it acquires a tangential velocity Vo at time t = 0.

(a) The velocity of the centre of the disc becomes zero for the first time at time t0. Find t0
(b) Find speed of the small body at time t03
The correct Answer is:(a) t0=2πRV0
(b) V02
Step by step video, text & image solution for A small body of mass m is at rest inside a narrow groove carved in a disc. Groove is a circle of radius R concentric to the disc. Mass of the disc is also m . The disc lies on a smooth horizontal floor. The small body is given a sharp impulse so that it acquires a tangential velocity Vo at time t = 0. (a) The velocity of the centre of the disc becomes zero for the first time at time t_(0). Find t_(0) (b) Find speed of the small body at time (t_(0))/(3) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Find the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
View SolutionA disc of mass m is moving with constant speed v0 on a smooth horizontal table. Another disc of mass M is placed on the table at rest as shown in the figure. If the collision is elastic, find the velocity of the disc after collision. Both disc lie on the same horizontal plane of the table.

View Solution
Knowledge Check
A disc has mass 'M' and radius 'R'. How much tangential force should be applied to the rim of the disc, so as to rotate with angular velocity 'ω' in time 't' ?
AMRω4tBMRω2tCMRωtDMRωtOut of a disc of mass M and radius R a concentric disc of mass m and radius r is removed. The M.I. of the remaining part about the symmetric axis will be :
A(M−m)(R+r)2/2B(M−m)(R2−r2)/2C(M−m)(R−r)2/2D(M−m)(R2+r2)/2A disc has mass 'M" and radius 'R'. How much tangential force should be applied to the rim of the disc so as to rotate with angular velocity ω in time 't'?
AMrω4tBMRω2tCMRωtDMRωt
A disc of mass M and radius R is kept flat on a smooth horizontal table. An insect of mass m alights on the periphery of the disc and begins to crawl along the edge.
(a) Describe the path of the centre of the disc.
For what value of mM the centre of the disc and the insect will follow the same path ?
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA disc has mass 'M' and radius 'R'. How much tangential force should be applied to the rim of the disc, so as to rotate with angular velocity 'ω' in time 't' ?
View SolutionCharge Q is uniformly distributed on the rim of a thin insulating disc of mass m which is initially at rest and placed on a smooth horizontal surface. What will be the angular velocity of the disc if a magnetic field B, perpendicular to the plane of the disc is switched on ?

View Solution
A disc of mass M and radius R is rolling purely with centre's velcity v0 on a flat horizontal floor when it hits a step in the floor of height R/4 The corner of the step is sufficiently rough to prevent any slippoing of the disc against itself. What is the velocity of the centre of the disc just after impact?
View Solution

