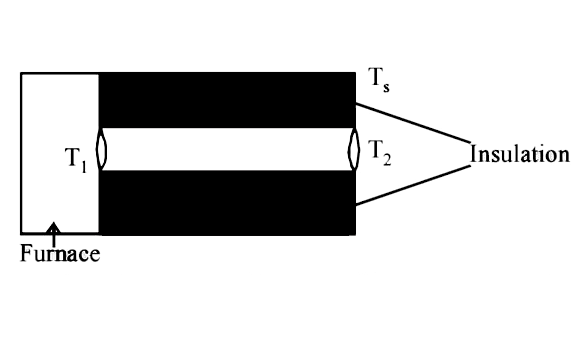
A cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is T0 and the furnace is maintained at T1=T0+ΔT1. The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained T2=T0+ΔT2[ΔT2<<T0]. The exposed surface of the rod has emissivity e. Prove that ΔT1 is proportional to ΔT2 and find the proportionality constant.
![A cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is T(0) and the furnace is maintained at T(1) = T(0) + DeltaT(1). The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained T(2) = T(0) + DeltaT(2) [DeltaT(2) ltlt T(0)]. The exposed surface of the rod has emissivity e. Prove that DeltaT(1) is proportional to DeltaT(2) and find the proportionality constant.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V02_C05_E05_045_Q01.png)
The correct Answer is:4eσLT30k+1
Step by step video, text & image solution for A cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is T_(0) and the furnace is maintained at T_(1) = T_(0) + DeltaT_(1). The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained T_(2) = T_(0) + DeltaT_(2) [DeltaT_(2) ltlt T_(0)]. The exposed surface of the rod has emissivity e. Prove that DeltaT_(1) is proportional to DeltaT_(2) and find the proportionality constant. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A cylinder rod of length 1, thermal conductivity K and area of cross section A has one end in the furnace at temperature T1 and the other end in surrounding at temperature T2. Surface of the rod exposed to the surrounding has emissivity e. Also T2=Ts+ΔTandTs>>ΔT. If T1−Ts∝ΔT,find the proportionality constant.
View Solution" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View Solution
Knowledge Check
A metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKLThe ends of a rod of uniform thermal conductivity are maintained at different (constant) temperatures. Afer the steady state is achieved:
Aheat flows in the rod from high temperature to low temperature even if the rod has nonuniform cross sectional area.Btemperature gradient along length is same even if the rod has non uniform cross sectional area.Cheat current is same even if the rod has nono-uniform cross sectional areaDif the rod has uniform cross sectional area the temperature is same at all points of the rod.All the rods have same conductance 'K' and same area of cross section 'A'. If ends A and C are maintained at temperature 2T0 and T0 respectively then which of the following is/are correct?
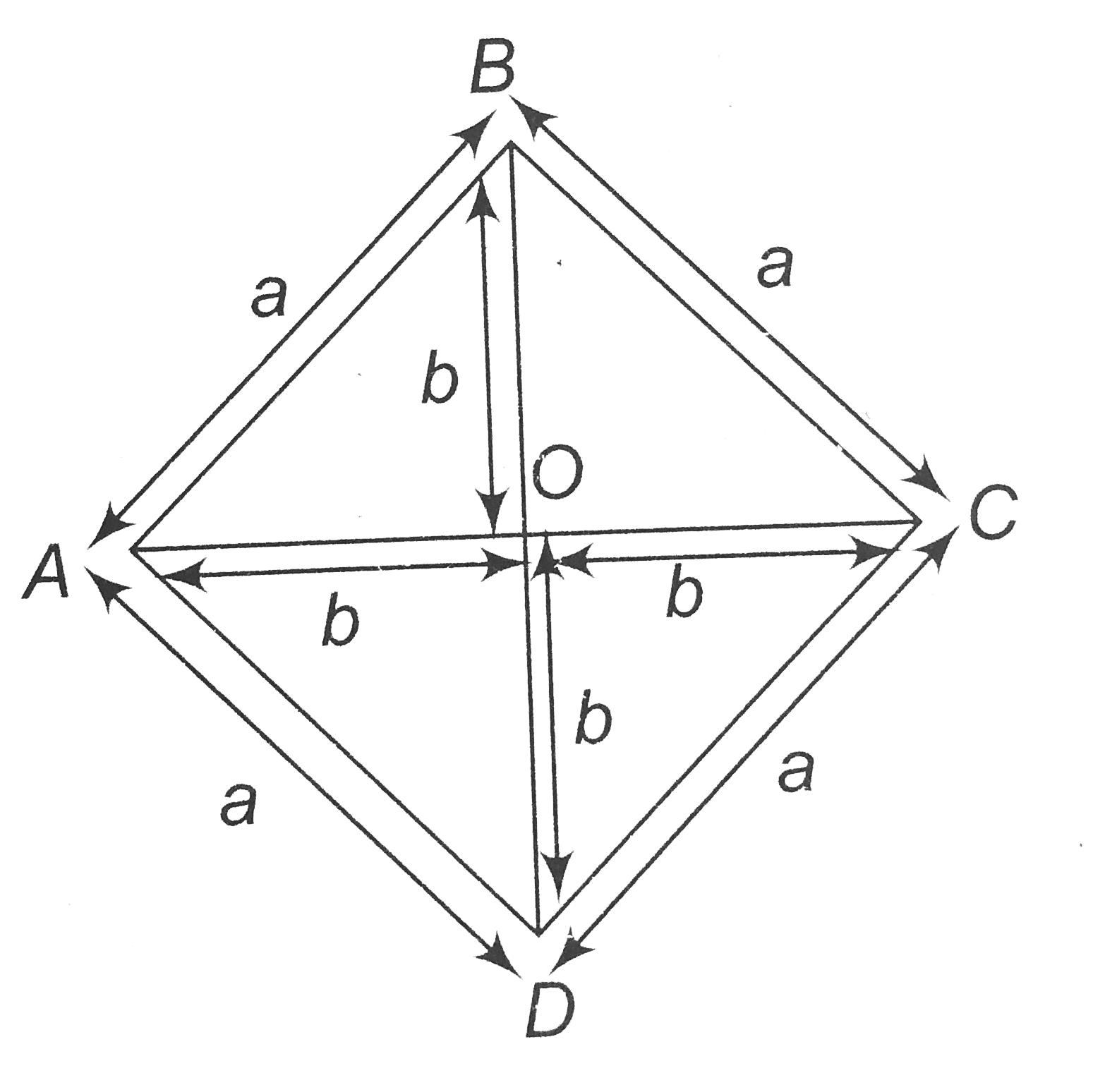 ARate of heat flow through ABC,AOCandADC is sameBRate of heat flow through BOandOD is not sameCTotal rate of heat flow from A to C is 3KAT02aDTemperature at junctions B,OandD are same
ARate of heat flow through ABC,AOCandADC is sameBRate of heat flow through BOandOD is not sameCTotal rate of heat flow from A to C is 3KAT02aDTemperature at junctions B,OandD are same
One end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of 100∘C. At the other end large quantity of ice is kept at 0∘C . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice.
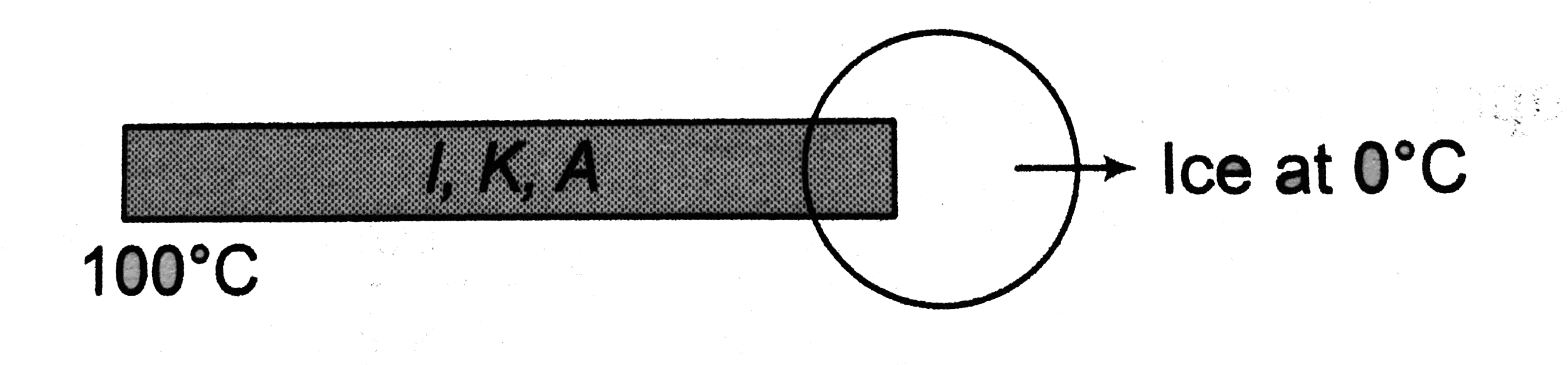 .
.
View SolutionA cylindrical rod of length l and cross - sectional radius r is placed at a distance of 50 r from a infrared point source S of power 1.25 kw as shown in the figure. The lateral surface of the rod is perfectly insulated from the surroundings . If the cross - section A absorbs 80 % of the incident energy and the temperature difference between the ends of the rod is constant , then the rate of heat flow through the rod in steady state is
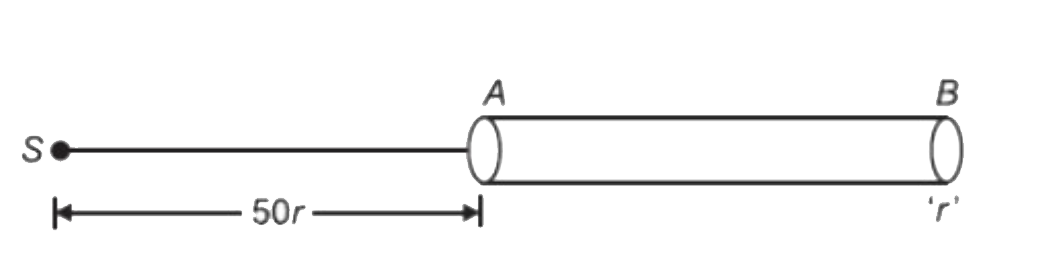
View SolutionTwo rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .
View SolutionOne end of conducting rod is maintained at temperature 50∘C and at the other end ice is melting at 0∘C. The rate of melting of ice is doubled if:
View SolutionTwo ends of area A of a uniform rod of thermal conductivity k are maintained at different but constant temperatures. At any point on the rod, the temperature gradient is dTdl. If I be the thermal current in the rod, then:
View Solution
