A sphere of radius R and charge Q is placed inside an imaginary sphere of radius 2R whose centre coincides with the given sphere. The flux related to imaginary sphere is:
Q∈0
Q2∈0
4Q∈0
2Q∈0
The correct Answer is:A
From flux =∫→E.→ds=Eqenclosed∈0∴ flux =Q∈0
Similar Questions
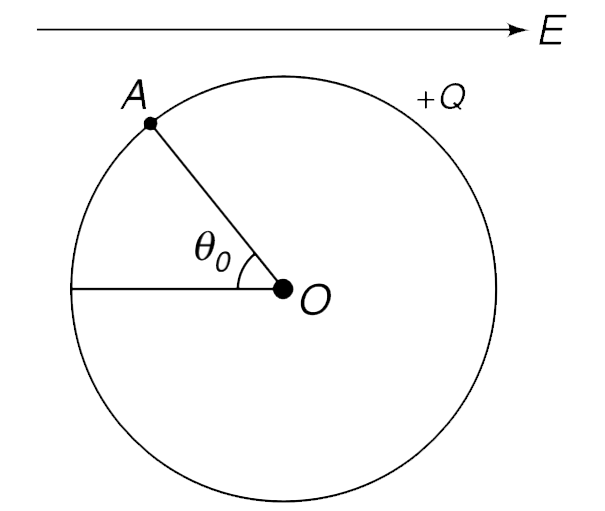
A conducting sphere of radius R having charge Q is placed in a uniform external field E. O is the centre of the sphere and A is a point on the sphere of the sphere such that AO makes an angle of θ0=60∘ with the opposite direction fo external field. calculate the potential at point A due to charge on the sphere only.
View SolutionA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View Solution
Knowledge Check
If a charge q is placed at the centre of imaginary sphere of radius r then the N.E.I. at a point on such a sphere is
A4πr2qBq4πr2C∈0kEDboth 'b' and 'c'A conducting sphere of radius r has a charge . Then .
Athe charge is uniformly distributed over its surface if there is an external electric field .BDistribution of charge over its surface will be non uniform if no external electric field exist in space,CElectric field strength inside the sphere will be equal to zero only when no external electric field existsDPotential at every point of the sphere must be sameA hollow sphere of radius 2R is charged to V volts and another smaller sphere of radius R is charged to V/2 volts. Now the smaller sphere is placed inside the bigger sphere without changing the net charge on each sphere. The potential difference between the two spheres would be
A3V2BV4CV2DV
A metallic sphere of radius R having charge Q is connected to an uncharged sphere of radius 3R. The amount of charge flown through connecting wire is
View SolutionA conducting sphere of radius R, carrying charge Q, lies inside uncharged conducting shell of radius 2R. If they are joined by a metal wire,
View SolutionAn electric dipole in placed completely inside a sphere in such a manner that centre of dipole coincides with the centre of sphere.
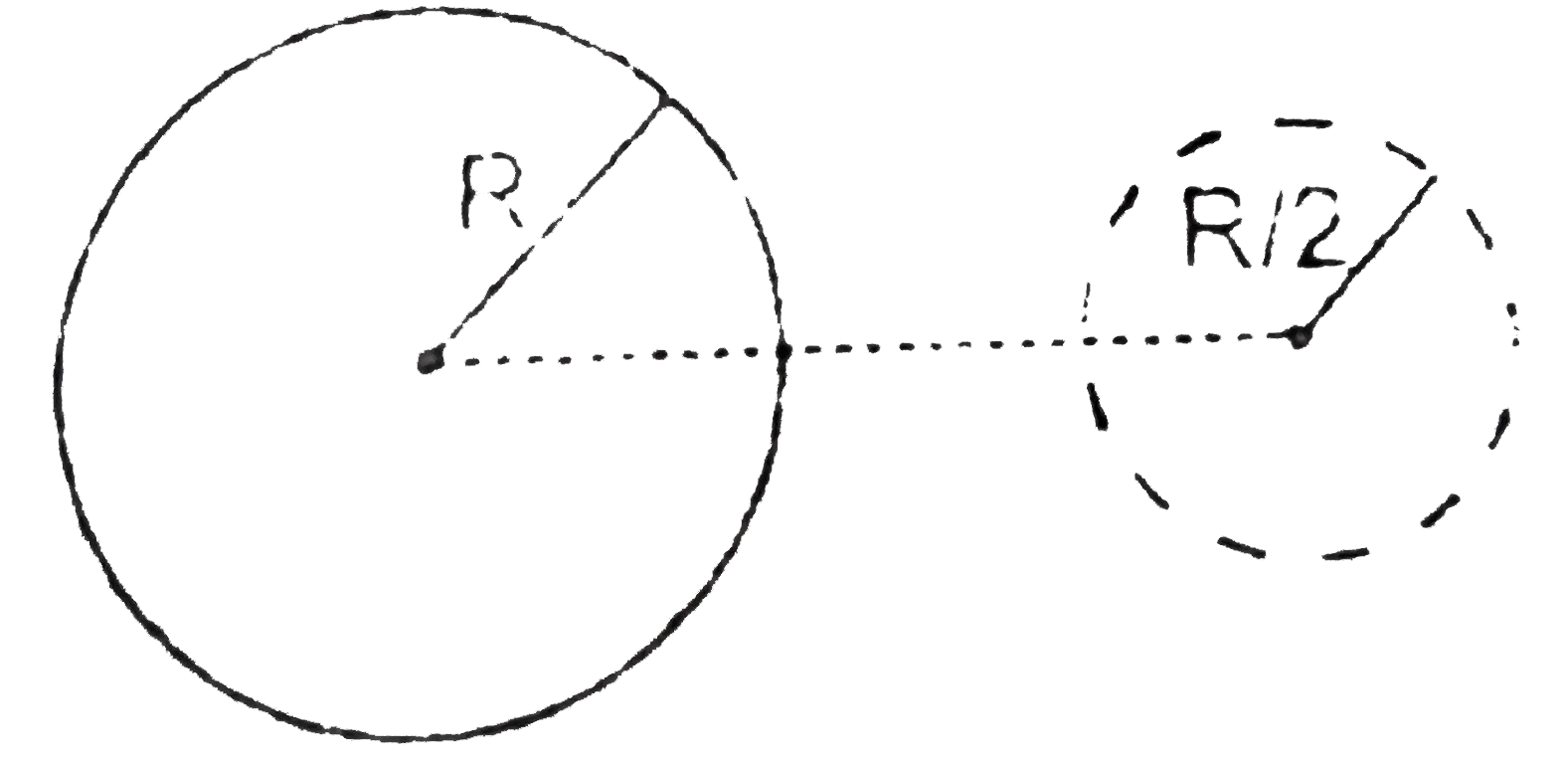
View SolutionA ring of radius R having a linear charge density λ moves towards a solid imaginary sphere of radius R2, so that the centre of ring passes through the centre of sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is
View SolutionAn unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R

View Solution

