A disc of mass M and radius R is rotating with angular velocity ω0 about a vertical axis passing through its centre (O). A man of mass M2 and height R2 is standing on the periphery. The man gradually lies down on the disc such that his head is at a distance R2 from the centre and his feet touching the edge of the disc. For simplicity assume that the man can be modelled as a thin rod of length R2. Calculate the angular speed (ω) of the platform after the man lies down.
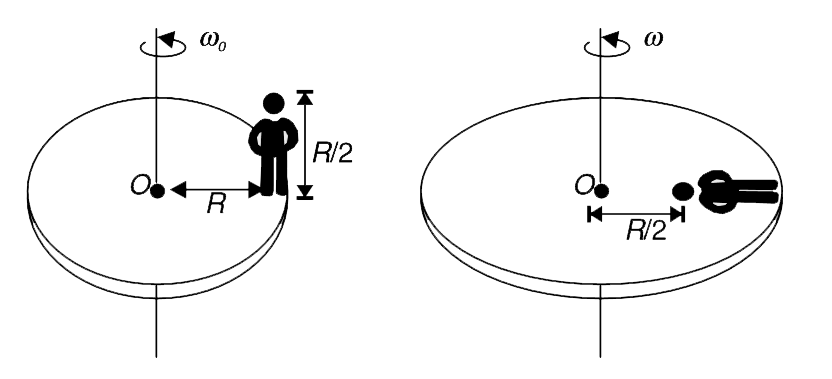
The correct Answer is:ω=2419ω0
Topper's Solved these Questions
Similar Questions
A uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

View SolutionA disc of mass M and radius r is rotating with an angular velocity ω. If gently, two masses m each are placed at a distance r/2 on either side of the axis of rotation, what will be the new angular velocity ?
View Solution
Knowledge Check
A uniform disc of mass M and radius R is rotating about a horizontal axis passing through its centre with angular velocity ω . A piece of mass m breaks from the disc and flies off vertically upwards. The angular speed of the disc will be
A(M−2m)ω(M−m)B(M+2m)ω(M+m)C(M−2m)ω(M+m)D(M+2m)ω(M−m)A circular disc of mass M and radius R is rotating with angular velocity ω . If two small spheres each of mass m are gently attached to two diametrically opposite points on the edge of the disc, then the new angular velocity of the disc will be
A(M+4mM)ωB(MM+4m)ωC(M+mM)ωD(MM+2m)ωA circular disc is rotating in horizontal plane about vertical axis passing through its centre without friction with a person standing on the disc at its edge. If the person gently walks to centre of disc then its angular velocity
AincreasesBdecreasesCdoes not changeDbecomes zero
The mass of a thin circular plate is M and its radius is R. About an axis in the plane of plate at a perpendicular distance R/2 from centre of plate, its moment of inertia is
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

View SolutionA uniform disc of mass M and radius R is rotating in a horizontal plane about an axis perpendicular to its plane with an angular velocity ω. Another disc of mass M/3 and radius R/2 is placed gently on the first disc coaxial. Then final angular velocity of the system is
View Solution

